复杂度分析

1. 衡量算法性能的标准

数据结构和算法本身解决的是“快”和“省”的问题，即如何让代码运行得更快，如何让代码更省存储空间。所以，执行效率是算法一个非常重要的考量指标。那如何来衡量算法代码的执行效率呢？那就用要时间复杂度、空间复杂度分析。其实，只要讲到数据结构与算法，就一定离不开时间、空间复杂度分析。

（1）为什么需要复杂度分析？

代码运行时，通过统计、监控，就能得到算法执行的时间和占用的内存大小。为什么还要做时间、空间复杂度分析呢？这种分析方法能比运行一遍得到的数据更准确吗？

首先，这种评估算法执行效率的方法是正确的。但是，这种统计方法有非常大的局限性：

• **测试结果非常依赖测试环境：**测试环境中硬件的不同会对测试结果有很大的影响。比如，我们拿同样一段代码，分别用Intel Core i9 处理器和 Intel Core i3 处理器来运行，不用说，i9 处理器要比 i3 处理器执行的速度快很多。还有，比如原本在这台机器上 a 代码执行的速度比 b 代码要快，等我们换到另一台机器上时，可能会有截然相反的结果。
• **测试结果受数据规模的影响很大：**对同一个排序算法，待排序数据的有序度不一样，排序的执行时间就会有很大的差别。极端情况下，如果数据已经是有序的，那排序算法不需要做任何操作，执行时间就会非常短。除此之外，如果测试数据规模太小，测试结果可能无法真实地反应算法的性能。比如，对于小规模的数据排序，插入排序可能反倒会比快速排序要快！

所以，我们需要一个不用具体的测试数据来测试，就可以粗略地估计算法的执行效率的方法。这就是时间复杂度、空间复杂度分析方法。

（2）大 O 复杂度表示法

复杂度是一个关于输入数据量 n 的函数。假设代码复杂度是 f(n)，那么就用个大写字母 O 和括号，把 f(n) 括起来就可以了，即 O(f(n))。例如，O(n) 表示的是，复杂度与计算实例的个数 n 线性相关；O(logn) 表示的是，复杂度与计算实例的个数 n 对数相关，这就是大 O 时间复杂度。

大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

通常，复杂度的计算方法遵循以下几个原则：

• 复杂度与具体的常系数无关，例如 O(n) 和 O(2n) 表示的是同样的复杂度。O(2n) 等于 O(n+n)，也等于 O(n) + O(n)。也就是说，一段 O(n) 复杂度的代码只是先后执行两遍 O(n)，其复杂度是一致的。
• 多项式级的复杂度相加的时候，选择高者作为结果，例如 O(n²)+O(n) 和 O(n²) 表示的是同样的复杂度。O(n²)+O(n) = O(n²+n)。随着 n 越来越大，二阶多项式的变化率是要比一阶多项式更大的。因此，只需要通过更大变化率的二阶多项式来表征复杂度就可以了。

值得一提的是，O(1) 也是表示一个特殊复杂度，含义为某个任务通过有限可数的资源即可完成。此处有限可数的具体意义是，与输入数据量 n 无关。

下面就分别来看看时间复杂度和空间复杂度是如何衡量的。

2. 时间复杂度分析

一般做算法复杂度分析的时候，遵循下面的技巧：

（1）只关注循环执行次数最多的一段代码

大 O 这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级即可。所以，在分析一个算法、一段代码的时间复杂度时，也只关注循环执行次数最多的那一段代码即可。这段核心代码执行次数的 n 的量级，就是整段要分析代码的时间复杂度。

下面来看一个例子：

function cal(n) {
  let sum = 0
  for (let i = 0; i <= n; ++i) {
    sum = sum + i
  }
  return sum
}

其中第 2 行代码是常量级的执行时间，与 n 的大小无关，所以对于复杂度并没有影响。循环执行次数最多的是第 4 行代码，这行代码被执行了 n 次，所以总的时间复杂度就是 O(n)。

（2）加法法则：总复杂度等于量级最大的那段代码的复杂度

下面来看一个例子：

function cal(n) {
  let sum_1 = 0
  for (let p = 1; p < 100; ++p) {
    sum_1 = sum_1 + p
  }

  let sum_2 = 0
  for (let q = 1; q < n; ++q) {
    sum_2 = sum_2 + q
  }

  let sum_3 = 0
  for (let i = 1; i <= n; ++i) {
    for (let j = 1; j <= n; ++j) {
      sum_3 = sum_3 + i * j
    }
  }

  return sum_1 + sum_2 + sum_3
}

这个代码分为三部分，分别是求 sum_1、sum_2、sum_3。可以分别分析每一部分的时间复杂度，然后把它们放到一起，再取一个量级最大的作为整段代码的复杂度。

第一段代码循环执行了 100 次，所以是一个常量的执行时间，跟 n 的规模无关。需要说明的是循环的次数只要是一个已知的数，跟 n 无关，照样也是常量级的执行时间。从时间复杂度的概念来说，它表示的是一个算法执行效率与数据规模增长的变化趋势，所以不管常量的执行时间多大，都可以忽略掉。因为它本身对增长趋势并没有影响。

第二段代码和第三段代码的时间复杂度分别是 O(n) 和 O(n2)，综合这三段代码的时间复杂度，取其中最大的量级。所以，整段代码的时间复杂度就为 O(n2)。也就是说：总的时间复杂度就等于量级最大的那段代码的时间复杂度。将这个规律抽象成公式就是：如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))。

（3）乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

下面看一个例子：

function cal(n) {
   let res = 0;
   for (let i = 1; i < n; ++i) {
     res = res + f(i);
   }
 }

 function f(int n) {
    let sum = 0;
    for (let i = 1; i < n; ++i) {
      sum = sum + i;
    }
    return sum;
 }

可以看到，如果cal方法中还有f函数，所以 cal() 函数的时间复杂度就是，T(n) = T1(n) * T2(n) = O(n*n) = O(n2)。

乘法法则看成是**嵌套循环，**将这个规律抽象成公式就是：如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))。

3. 常见的时间复杂度

常见时间复杂度：

• O(1)：基本运算 +、-、*、/、%、寻址
• O(logn)：二分查找，跟分治（Divide & Conquer）相关的基本上都是 logn
• O(n)：线性查找
• O(nlogn)：归并排序，快速排序的期望复杂度，基于比较排序的算法下界
• O(n²)：冒泡排序，插入排序，朴素最近点对
• O(n³)：Floyd 最短路，普通矩阵乘法
• O(2ⁿ)：枚举全部子集
• O(n!)：枚举全排列

随着问题规模 n 的不断增大，上述时间复杂度不断增大，算法的执行效率越低。

（1）O(1)

O(1) 只是常量级时间复杂度的一种表示方法，并不是指只执行了一行代码。比如下面这段代码，它的时间复杂度也是 O(1）：

let i = 8
let j = 6
let sum = i + j

只要代码的执行时间不随 n 的增大而增长，这样代码的时间复杂度都记作 O(1)。一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

（2）O(logn)、O(nlogn)

对数阶时间复杂度非常常见，也是最难分析的一种时间复杂度。下面来看一个例子：

let i = 1
while (i <= n) {
  i = i * 2
}

这里第三行代码是循环执行次数最多的。所以，只要能计算出这行代码被执行了多少次，就能知道整段代码的时间复杂度。

从代码中可以看出，变量 i 的值从 1 开始取，每循环一次就乘以 2。当大于 n 时，循环结束。实际上，变量 i 的取值就是一个等比数列。它们应该是这样子：

所以，只要知道 x 值是多少，就知道这行代码执行的次数了。通过 2x=n 求解 x，x=log2n。所以，这段代码的时间复杂度就是 O(log2n)。

下面把代码稍微改下：

let i = 1
while (i <= n) {
  i = i * 3
}

这段代码的时间复杂度为 O(log3n)。实际上，不管是以 2 为底、以 3 为底，还是以 10 为底，都可以把所有对数阶的时间复杂度都记为 O(logn)。因为对数之间是可以互相转换的，log3n 就等于 log32 _ log2n，所以 O(log3n) = O(C _ log2n)，其中 C=log32 是一个常量。基于前面的理论：在采用大 O 标记复杂度的时候，可以忽略系数，即 O(Cf(n)) = O(f(n))。所以，O(log2n) 就等于 O(log3n)。因此，在对数阶时间复杂度的表示方法里，我们忽略对数的“底”，统一表示为 O(logn)。

如果一段代码的时间复杂度是 O(logn)，循环执行 n 遍，时间复杂度就是 O(nlogn) 了。而且，O(nlogn) 也是一种常见的算法时间复杂度。比如，归并排序、快速排序的时间复杂度都是 O(nlogn)。

（3）O(m+n)、O(m*n)

下面来看一种跟前面都不一样的时间复杂度，代码的复杂度由两个数据的规模来决定：

function cal(m, n) {
  let sum_1 = 0
  for (let i = 0; i < m; ++i) {
    sum_1 = sum_1 + i
  }
  let sum_2 = 0
  for (let j = 0; j < n; ++j) {
    sum_2 = sum_2 + j
  }
  return sum_1 + sum_2
}

可以看到，m 和 n 是表示两个数据规模，无法事先评估 m 和 n 谁的量级大，所以在表示复杂度时，就不能简单地利用加法法则，省略掉其中一个。所以，上面代码的时间复杂度就是 O(m+n)。

针对这种情况，原来的加法法则就不正确了，需要将加法规则改为：T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效：T1(m)_T2(n) = O(f(m) _ f(n))。

4. 时间复杂度分析进阶

上面介绍了最基本的时间复杂度分析的方法，下面来看复杂度分析的进阶知识点：

• 最好时间复杂度（best case time complexity）
• 最坏时间复杂度（worst case time complexity）
• 平均时间复杂度（average case time complexity）
• 均摊时间复杂度（amortized time complexity）

（1）最好、最坏时间复杂度

下面来看一个例子：

// n 表示数组 array 的长度
function find(array, n, x) {
  let pos = -1
  for (let i = 0; i < n; ++i) {
    if (array[i] == x) pos = i
  }
  return pos
}

可以看到，这段代码要实现的功能是，在一个无序的数组（array）中，查找变量 x 出现的位置。如果没有找到，就返回 -1。这段代码的复杂度是 O(n)，其中，n 代表数组的长度。

在数组中查找一个数据时，并不需要每次都把整个数组都遍历一遍，因为有可能中途找到就可以提前结束循环了。但是，这段代码写得不够高效。可以这样进行优化：

// n 表示数组 array 的长度
function find(array, n, x) {
  let pos = -1
  for (let i = 0; i < n; ++i) {
    if (array[i] == x) {
      pos = i
      break
    }
  }
  return pos
}

那优化完之后，这段代码的时间复杂度还是 O(n) 吗？很显然，上面的分析方法，解决不了这个问题。

因为，要查找的变量 x 可能出现在数组的任意位置。如果数组中第一个元素正好是要查找的变量 x，那就不需要继续遍历剩下的 n-1 个数据了，那时间复杂度就是 O(1)。但如果数组中不存在变量 x，那就需要把整个数组都遍历一遍，时间复杂度就成了 O(n)。所以，不同的情况下，这段代码的时间复杂度是不一样的。

为了表示代码在不同情况下的不同时间复杂度，需要引入三个概念：最好时间复杂度、最坏时间复杂度和平均时间复杂度。

• 最好情况时间复杂度就是，在最理想的情况下，执行这段代码的时间复杂度。在最理想的情况下，要查找的变量 x 正好是数组的第一个元素，这个时候对应的时间复杂度就是最好情况时间复杂度。
• 最坏情况时间复杂度就是，在最糟糕的情况下，执行这段代码的时间复杂度。如果数组中没有要查找的变量 x，需要把整个数组都遍历一遍才行，所以这种最糟糕情况下对应的时间复杂度就是最坏情况时间复杂度。

（2）平均时间复杂度

最好时间复杂度和最坏时间复杂度对应的都是极端情况下的代码复杂度，发生的概率其实并不大。为了更好地表示平均情况下的复杂度，需要引入另一个概念：平均时间复杂度。

借助上面的例子，要查找的变量 x 在数组中的位置，有 n+1 种情况：在数组的 0～n-1 位置中和不在数组中。我们把每种情况下，查找需要遍历的元素个数累加起来，然后再除以 n+1，就可以得到需要遍历的元素个数的平均值，即：

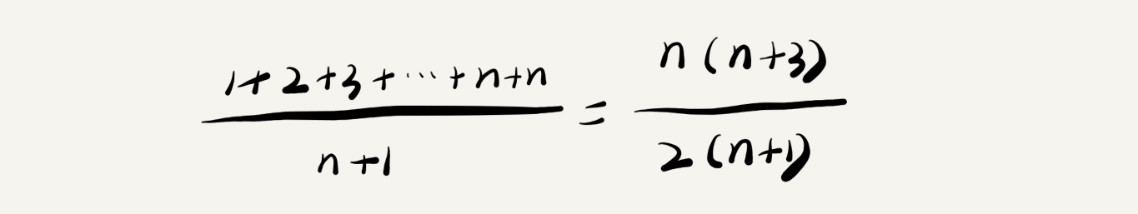
在时间复杂度的大 O 标记法中，可以省略掉系数、低阶、常量，所以，把这个公式简化之后，得到的平均时间复杂度就是 O(n)。

这个结论虽然是正确的，但是计算过程稍微有点儿问题。这 n+1 种情况，出现的概率并不是一样的。要查找的变量 x，要么在数组里，要么就不在数组里。这两种情况对应的概率统计起来很麻烦，我们假设在数组中与不在数组中的概率都为 1/2。另外，要查找的数据出现在 0～n-1 这 n 个位置的概率也是一样的，为 1/n。所以，根据概率乘法法则，要查找的数据出现在 0～n-1 中任意位置的概率就是 1/(2n)。

因此，前面的推导过程中存在的最大问题就是，没有将各种情况发生的概率考虑进去。如果把每种情况发生的概率也考虑进去，那平均时间复杂度的计算过程就变成了这样：

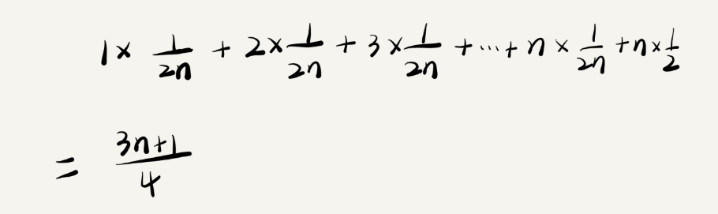
这个值就是概率论中的加权平均值，也叫作期望值，所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。

引入概率之后，前面那段代码的加权平均值为 (3n+1)/4。用大 O 表示法来表示，去掉系数和常量，这段代码的加权平均时间复杂度仍然是 O(n)。

实际上，在大多数情况下，并不需要区分最好、最坏、平均情况时间复杂度三种情况。而使用一个复杂度就可以满足需求了。只有同一块代码在不同的情况下，时间复杂度有量级的差距，才会使用这三种复杂度表示法来区分。

（3）均摊时间复杂度

下面来看看均摊时间复杂度的概念，以及它对应的分析方法，摊还分析（或者叫平摊分析）。

均摊时间复杂度，听起来跟平均时间复杂度很像。在大部分情况下，我们并不需要区分最好、最坏、平均三种复杂度。平均复杂度只在某些特殊情况下才会用到，而均摊时间复杂度应用的场景比它更加特殊、更加有限。

下面来看一个例子：

// array 表示一个长度为 n 的数组
// 代码中的 array.length 就等于 n
const array = new Array(n)
let count = 0
function insert(val) {
  if (count == array.length) {
    let sum = 0
    for (let i = 0; i < array.length; ++i) {
      sum = sum + array[i]
    }
    array[0] = sum
    count = 1
  }
  array[count] = val
  ++count
}

这段代码实现了一个往数组中插入数据的功能。当数组满了之后，也就是代码中的 count == array.length 时，就用 for 循环遍历数组求和，并清空数组，将求和之后的 sum 值放到数组的第一个位置，然后再将新的数据插入。但如果数组一开始就有空闲空间，则直接将数据插入数组。

最理想的情况下，数组中有空闲空间，只需要将数据插入到数组下标为 count 的位置就可以了，所以最好情况时间复杂度为 O(1)。最坏的情况下，数组中没有空闲空间了，需要先做一次数组的遍历求和，然后再将数据插入，所以最坏情况时间复杂度为 O(n)。

平均时间复杂度是 O(1)。可以通过前面讲的概率论的方法来分析：假设数组的长度是 n，根据数据插入的位置的不同，可以分为 n 种情况，每种情况的时间复杂度是 O(1)。除此之外，还有一种“额外”的情况，就是在数组没有空闲空间时插入一个数据，这个时候的时间复杂度是 O(n)。而且，这 n+1 种情况发生的概率一样，都是 1/(n+1)。所以，根据加权平均的计算方法，求得的平均时间复杂度就是：

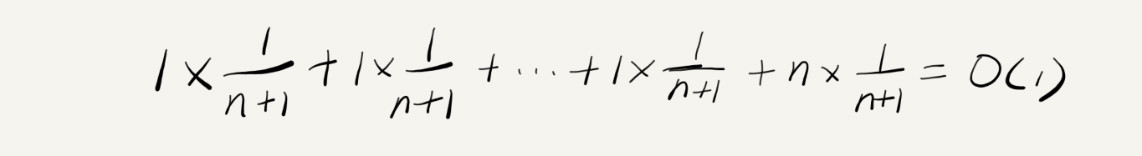
这里的平均复杂度分析其实并不需要这么复杂，不需要引入概率论的知识。先来对比一下这个 insert() 的例子和前面那个 find() 的例子，这两者有很大差别。

• 首先，find() 函数在极端情况下，复杂度才为 O(1)。但 insert() 在大部分情况下，时间复杂度都为 O(1)。只有个别情况下，复杂度才比较高，为 O(n)。这是 insert()第一个区别于 find() 的地方。
• 第二个不同的地方。对于 insert() 函数来说，O(1) 时间复杂度的插入和 O(n) 时间复杂度的插入，出现的频率是非常有规律的，而且有一定的前后时序关系，一般都是一个 O(n) 插入之后，紧跟着 n-1 个 O(1) 的插入操作，循环往复。

所以，针对这样一种特殊场景的复杂度分析，并不需要像之前讲平均复杂度分析方法那样，找出所有的输入情况及相应的发生概率，然后再计算加权平均值。

针对这种特殊的场景，引入了一种更加简单的分析方法：摊还分析法，通过摊还分析得到的时间复杂度叫均摊时间复杂度。

那如何使用摊还分析法来分析算法的均摊时间复杂度呢？

以数组中插入数据为例。每一次 O(n) 的插入操作，都会跟着 n-1 次 O(1) 的插入操作，所以把耗时多的那次操作均摊到接下来的 n-1 次耗时少的操作上，均摊下来，这一组连续的操作的均摊时间复杂度就是 O(1)。这就是均摊分析的大致思路。

均摊时间复杂度和摊还分析应用场景比较特殊，所以并不会经常用到。下面来看一下它们的应用场景：

对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有个别情况下时间复杂度比较高，而且这些操作之间存在前后连贯的时序关系，这个时候，我们就可以将这一组操作放在一块儿分析，看是否能将较高时间复杂度那次操作的耗时，平摊到其他那些时间复杂度比较低的操作上。而且，在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。

5. 空间复杂度

时间复杂度的全称是渐进时间复杂度，表示算法的执行时间与数据规模之间的增长关系。类比一下，空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。

下面来看一个例子：

function print(int n) {
  const a = new Array(n);
  for (let i = 0; i <n; ++i) {
    a[i] = i * i;
  }
  for (i = n - 1; i >= 0; --i) {
    console.log(a[i])
  }
}

可以看到，第 3 行代码申请了一个空间存储变量 i，但是它是常量阶的，跟数据规模 n 没有关系，所以可以忽略。第 2 行申请了一个大小为 n 的数组，除此之外，剩下的代码都没有占用更多的空间，所以整段代码的空间复杂度就是 O(n)。

常见的空间复杂度就是 O(1)、O(n)、O(n2 )，像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。

6. 时间转空间复杂度

上面介绍了衡量代码效率的方法。那么，针对这些低效代码，该如何提高它们的效率呢？下面就来看看对于时间复杂度和空间复杂度之间转换的内容，以此来提高代码的效率。

在面试的过程中，遇到考察手写代码的场景，通常面试官会追问：“这段代码的时间复杂度或者空间复杂度，是否还有降低的可能性？”。其实，代码效率优化就是要将可行解提高到更优解，最终目标是：要采用尽可能低的时间复杂度和空间复杂度，去完成一段代码的开发。

（1）时间昂贵、空间廉价

一段代码会消耗计算时间、资源空间，从而产生时间复杂度和空间复杂度，将时间复杂度和空间复杂进行一下对比会发现一个重要的现象。

假设一段代码经过优化后，虽然降低了时间复杂度，但依然需要消耗非常高的空间复杂度。 例如，对于固定数据量的输入，这段代码需要消耗几十 G 的内存空间，很显然普通计算机根本无法完成这样的计算。如果一定要解决的话，一个最简单粗暴的办法就是，购买大量的高性能计算机，来弥补空间性能的不足。

反过来，假设一段代码经过优化后，依然需要消耗非常高的时间复杂度。 例如，对于固定数据量的输入，这段代码需要消耗 1 年的时间去完成计算。如果在跑程序的 1 年时间内，出现了断电、断网或者程序抛出异常等预期范围之外的问题，那很可能造成 1 年时间浪费的惨重后果。很显然，用 1 年的时间去跑一段代码，对开发者和运维者而言都是极不友好的。

这告诉我们一个很现实问题：代码效率的瓶颈可能发生在时间或者空间两个方面。如果是缺少计算空间，花钱买服务器就可以了。这是个花钱就能解决的问题。相反，如果是缺少计算时间，只能投入宝贵的时间去跑程序。即使有再多的钱、再多的服务器，也是毫无用处。相比于空间复杂度，时间复杂度的降低就显得更加重要了。因此会发现这样的结论：空间是廉价的，而时间是昂贵的。

（2）数据结构连接时空

假定在不限制时间、也不限制空间的情况下，可以完成某个任务的代码的开发。这就是暴力解法，更是程序优化的起点。

例如，如果要在 100 以内的正整数中，找到同时满足以下两个条件的最小数字：

• 能被 3 整除；
• 除 5 余 2。

最暴力的解法就是，从 1 开始到 100，每个数字都做一次判断。如果这个数字满足了上述两个条件，则返回结果。这是一种不计较任何时间复杂度或空间复杂度的、最直观的暴力解法。当有了最暴力的解法后，就需要评估当前暴力解法的复杂度了。如果复杂度比较低或者可以接受。可如果暴力解法复杂度比较高，那就要考虑采用程序优化的方法去降低复杂度了。

为了降低复杂度，一个直观的思路是：梳理程序，看其流程中是否有无效的计算或者无效的存储。我们需要从时间复杂度和空间复杂度两个维度来考虑。常用的降低时间复杂度的方法有递归、二分法、排序算法、动态规划等。而降低空间复杂度的方法，就要围绕数据结构做文章了。

降低空间复杂度的核心思路就是，能用低复杂度的数据结构能解决问题，就千万不要用高复杂度的数据结构。

经过了剔除无效计算和存储的处理之后，如果程序在时间和空间等方面的性能依然还有瓶颈，又该怎么办呢？如果可以通过某种方式，把时间复杂度转移到空间复杂度，就可以把无价的东西变成有价了。

在程序开发中，连接时间和空间的桥梁就是数据结构。对于一个开发任务，如果能找到一种高效的数据组织方式，采用合理的数据结构的话，那就可以实现时间复杂度的再次降低。同样的，这通常会增加数据的存储量，也就是增加了空间复杂度。

以上就是程序优化的最核心的思路：

• 第一步，暴力解法。在没有任何时间、空间约束下，完成代码任务的开发。
• 第二步，无效操作处理。将代码中的无效计算、无效存储剔除，降低时间或空间复杂度。
• 第三步，时空转换。设计合理数据结构，完成时间复杂度向空间复杂度的转移。

（3）时间换空间案例

假设有任意多张面额为 1 元、2 元、10 元的纸币，用它们凑出 100 元，求总共有多少种可能性。暴力解法如下：

function fn() {
  let count = 0
  for (let i = 0; i <= 100 / 10; i++) {
    for (let j = 0; j <= 100 / 2; j++) {
      for (let k = 0; k <= 100 / 1; k++) {
        if (i * 10 + j * 2 + k * 1 == 100) {
          count += 1
        }
      }
    }
  }
  return count
}

在这段代码中，使用了 3 层的 for 循环。从结构上来看，是很显然的 O( n³ ) 的时间复杂度。然而，代码中最内层的 for 循环是多余的。因为，当你确定了要用 i 张 10 元和 j 张 2 元时，只需要判断用有限个 1 元能否凑出 100 - 10* i - 2* j 元即可。因此，代码改写如下：

function fn() {
  let count = 0
  for (let i = 0; i <= 100 / 10; i++) {
    for (let j = 0; j <= 100 / 2; j++) {
      if (100 - i * 10 - j * 2 >= 0 && (100 - i * 10 - j * 2) % 2 == 0) {
        count += 1
      }
    }
  }
  return count
}

改造之后，代码的结构由 3 层 for 循环，变成了 2 层 for 循环。很显然，时间复杂度就变成了O(n²) 。这样的代码改造，就是利用了将代码中的无效计算、无效存储剔除，降低时间或空间复杂度。

再看第二个例子。查找一个数组中出现次数最多的那个元素。例如，输入数组 a = [1,2,3,4,5,5,6 ] 中，查找出现次数最多的元素。从数组中可以看出，只有 5 出现了 2 次，其余都是 1 次，所以输出 5。

最笨的方法就是采用两层的 for 循环完成计算。第一层循环，对数组每个元素遍历。第二层循环，则是对第一层遍历的数字，去遍历计算其出现的次数。这样，全局再同时缓存一个出现次数最多的元素即可，代码如下：

function fn() {
  let a = [1, 2, 3, 4, 5, 5, 6]
  let res = ''
  for (let i = 0; i < a.length; i++) {
    let count = 0
    for (let j = 0; j < a.length; j++) {
      if (a[i] == a[j]) {
        count += 1
      }
      count > res ? (res = a[i]) : (res = res)
    }
  }
  return res
}

这段代码中采用了两层的 for 循环，很显然时间复杂度就是 O(n²)。而且代码中，几乎没有冗余的无效计算。如果还需要再去优化，就要考虑采用一些数据结构方面的手段，来把时间复杂度转移到空间复杂度了。

我们可以通过一次 for 循环，在循环的过程中，同步记录下每个元素出现的次数。最后，再通过查找次数最大的元素，就得到了结果。

具体而言，定义一个 key-value 结构的字典，用来存放元素-出现次数的 key-value 关系。那么首先通过一次循环，将数组转变为元素-出现次数的一个字典。接下来，再去遍历一遍这个字典，找到出现次数最多的那个元素，就能找到最后的结果了。具体代码如下：

function fn() {
  let a = [1, 2, 3, 4, 5, 5, 6]
  let map = {},
    res = ''

  for (let i = 0; i < a.length; i++) {
    map[a[i]] ? (map[a[i]] += 1) : (map[a[i]] = 1)
  }

  for (let key in map) {
    map[key] > res ? (res = key) : (res = res)
  }
  return res
}

这段代码有两个 for 循环。不过，这两个循环不是嵌套关系，而是顺序执行关系。其中，第一个循环实现了数组转字典的过程，也就是 O(n) 的复杂度。第二个循环再次遍历字典找到出现次数最多的那个元素，也是一个 O(n) 的时间复杂度。

因此，总体的时间复杂度为 O(n) + O(n)，就是 O(2n)，根据复杂度与具体的常系数无关的原则，也就是O(n) 的复杂度。空间方面，由于定义了 key-value 字典，其字典元素的个数取决于输入数组元素的个数。因此，空间复杂度增加为 O(n)。

这段代码就是通过采用更复杂、高效的数据结构，完成了时空转移，提高了空间复杂度，让时间复杂度再次降低。

题目分析

二分查找-704

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4 示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1

链接：leetcode-cn.com/problems/binary-search

思路

二分查找是个很经典的算法了，它的一个典型的特点就是“思路容易，细节非常易错”。

这里就主要讲讲代码里的细节吧：

1. 首先，为什么是 while (left <= right) 而不是 while (left < right)？ 这是因为要考虑到 left 和 right 相等的情况，也就是查找区间里只有一个值。
2. 为什么 left = mid + 1，这个 +1 是什么？ 这是因为 mid 位置的值已经查找过了，可以往右边跳一位。
3. 什么情况 left 会超出 right？如果二分查找到的值一直小于目标值，left会不断右移，直到最后数组区间里只有一个值，如果此时这个目标值还是大于这个值，left 会继续加一，此时 left 会超过 right。
4. 反之，则 right 会超出 left。

var search = function (nums, target) {
  // 定义左右指针
  let left = 0
  let right = nums.length - 1

  // 当左指针小于等于右指针时，继续查找
  while (left <= right) {
    // 计算中间索引
    const mid = Math.round((left + right) / 2)

    // 检查中间元素是否是目标值
    if (nums[mid] === target) {
      return mid // 找到目标值，返回索引
    } else if (nums[mid] < target) {
      // 如果目标值大于中间元素，移动左指针
      left = mid + 1
    } else {
      // 如果目标值小于中间元素，移动右指针
      right = mid - 1
    }
  }

  // 如果未找到目标值，返回-1
  return -1
}

移动零-283

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

输入: [0, 1, 0, 3, 12]
输出: [1, 3, 12, 0, 0]

说明:

必须在原数组上操作，不能拷贝额外的数组。尽量减少操作次数。 leetcode-cn.com/problems/move-zeroes

思路

暴力法

先遍历一次，找出所有 0 的下标，然后删除掉所有 0 元素，再 push 相应的 0 的个数到末尾。

var moveZeroes = function (nums) {
  let zeros = []
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] === 0) {
      zeros.push(i)
    }
  }
  for (let j = zeros.length - 1; j >= 0; j--) {
    nums.splice(zeros[j], 1)
  }
  for (let j = 0; j < zeros.length; j++) {
    nums.push(0)
  }
  return nums
}

双指针

慢指针 j 从 0 开始，当快指针 i 遍历到非 0 元素的时候，i 和 j 位置的元素交换,然后把 j + 1。

也就是说，快指针 i 遍历完毕后, [0, j) 区间就存放着所有非 0 元素，而剩余的[j,n]区间再遍历一次，用 0 填充满即可。

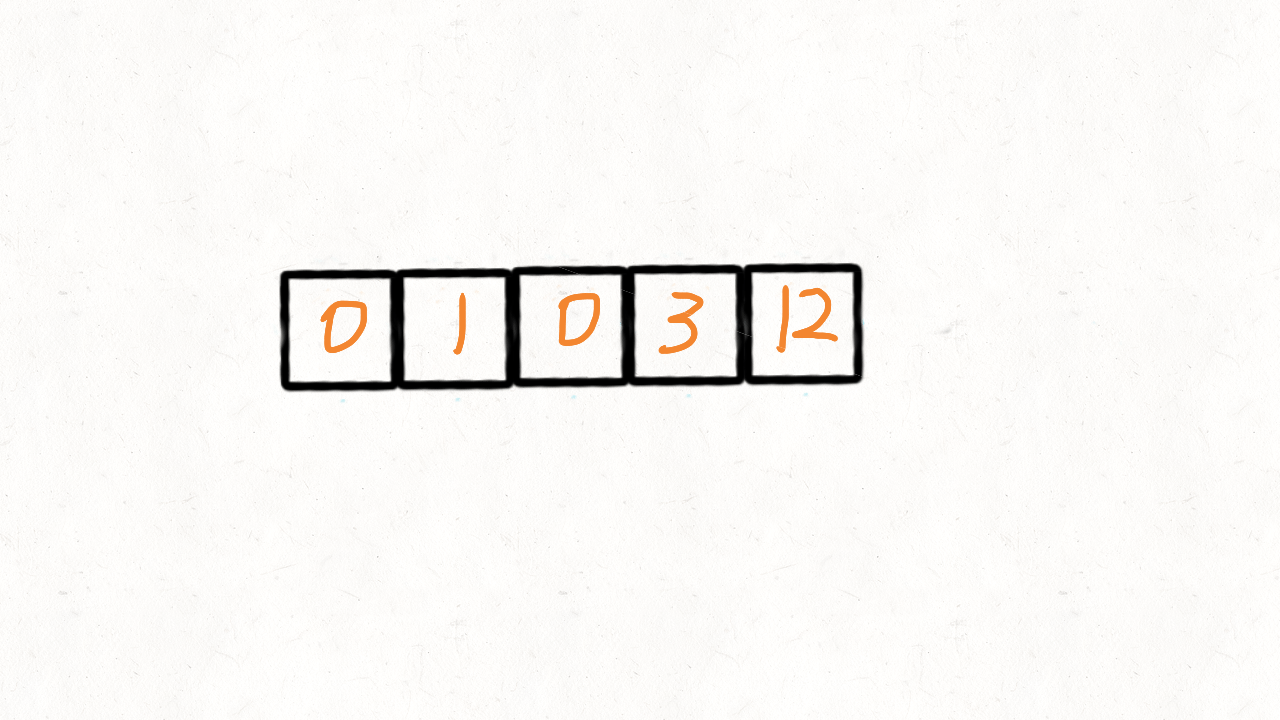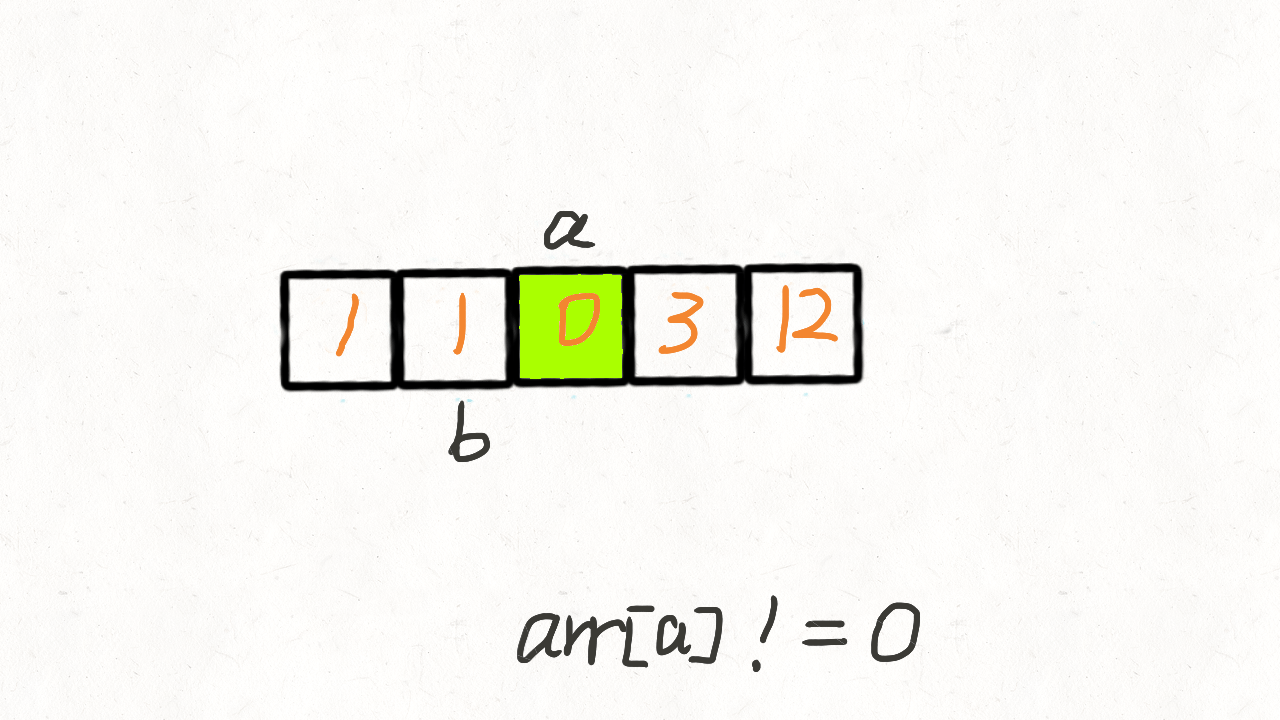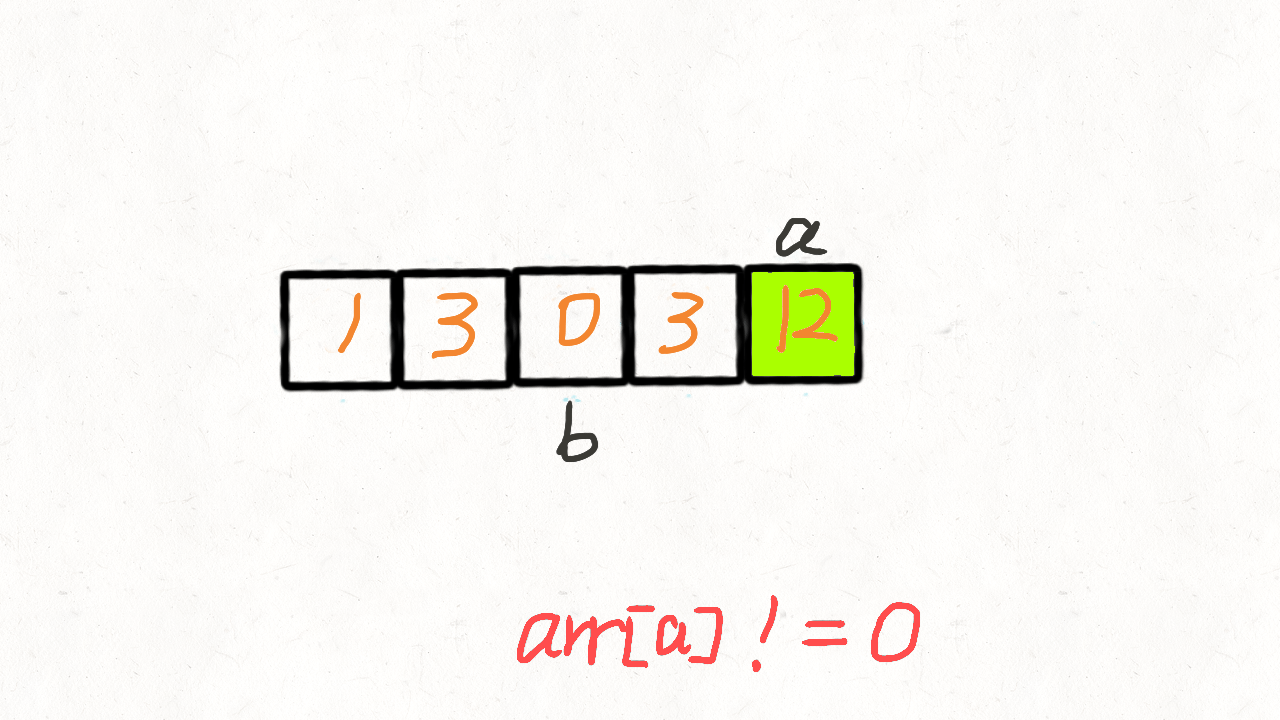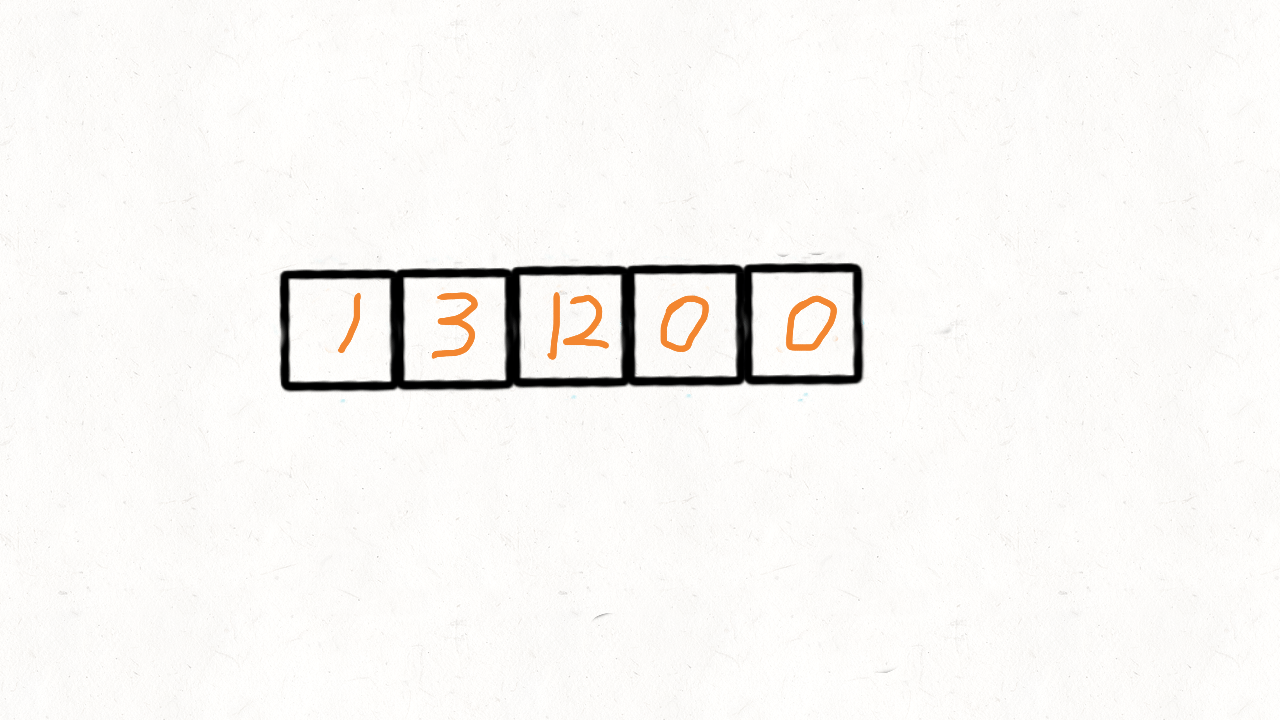
var moveZeroes = function (nums) {
  let j = 0
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] !== 0) {
      nums[j] = nums[i]
      j++
    }
  }
  while (j < nums.length) {
    nums[j] = 0
    j++
  }
}

双指针（交换位置）

在上面的算法里，快指针遍历完成后，还要遍历慢指针到末尾来填充 0。实际上这题只要遇 到非 0 元素，就把当前位置的值和慢指针位置 j 的值交换，然后只有此时 j 才 + 1，即 可完成。

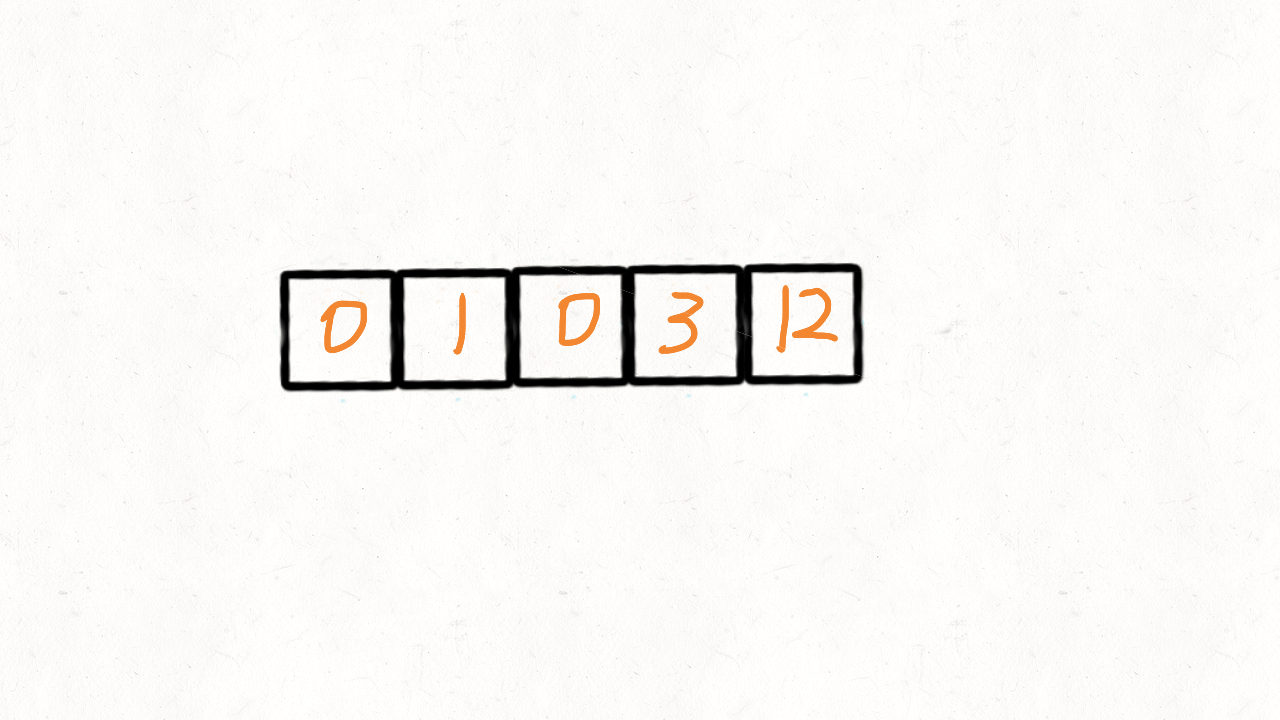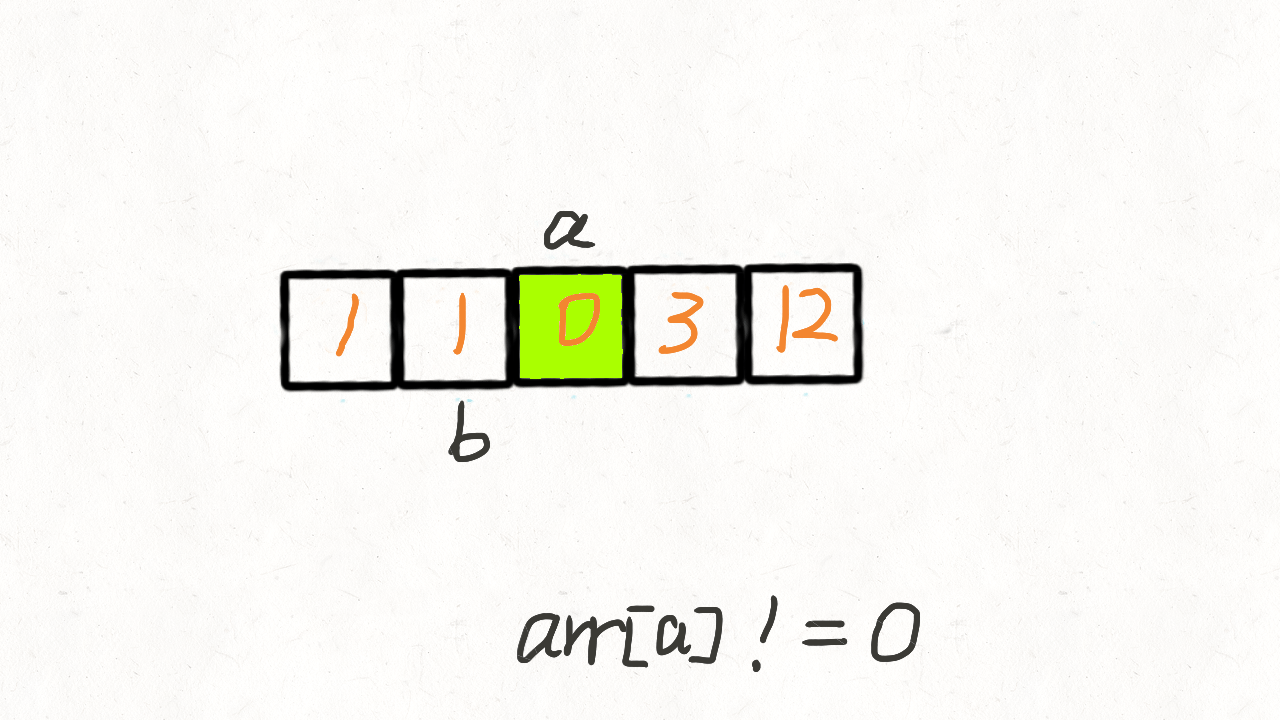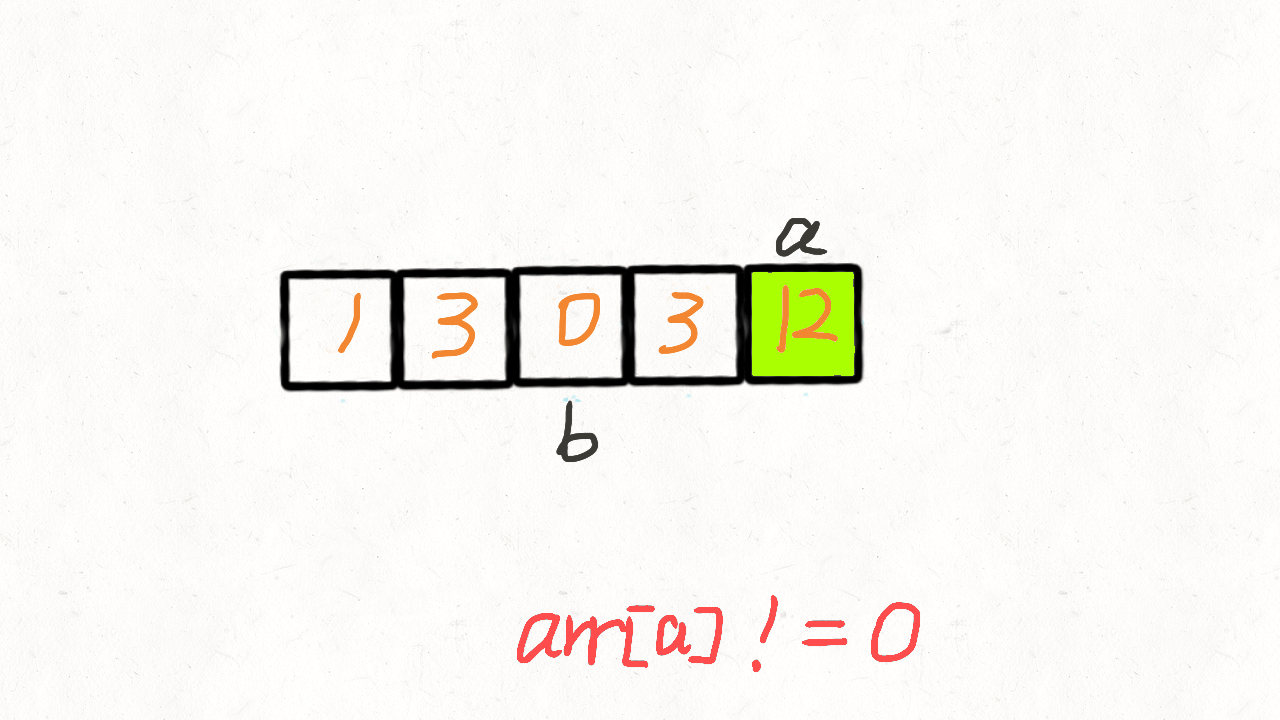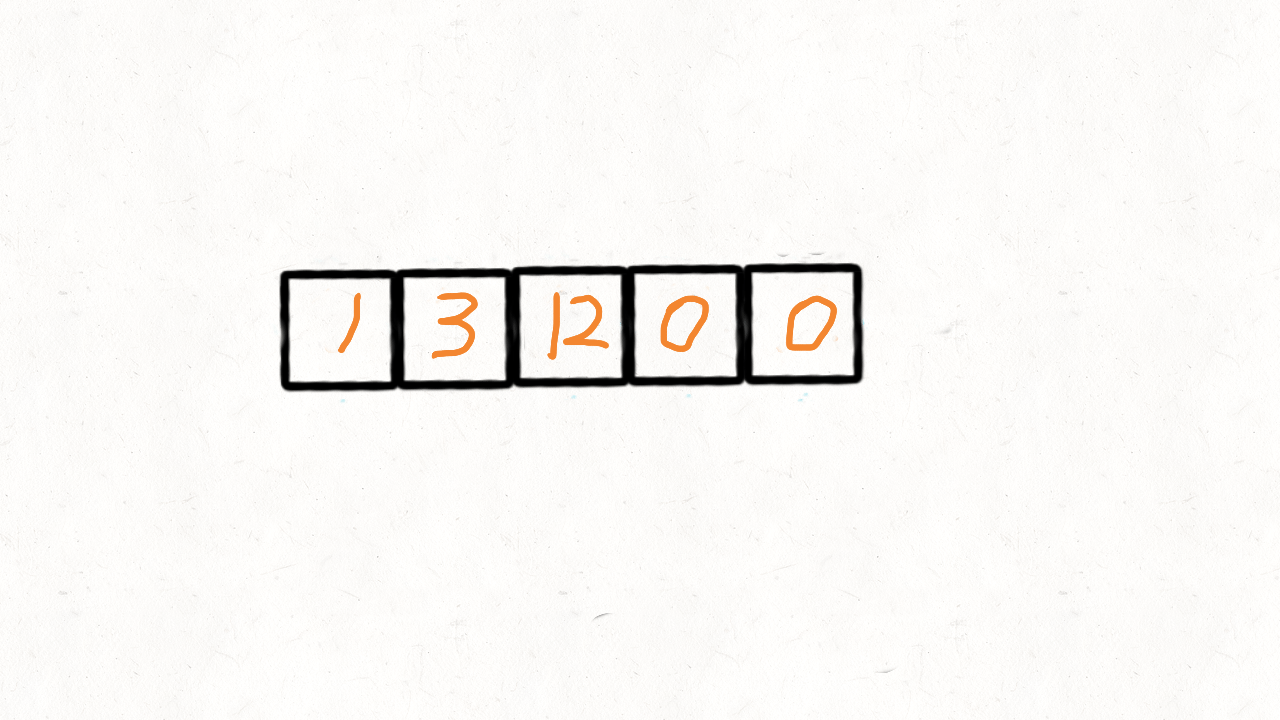
var moveZeroes = function (nums) {
  let j = 0
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] !== 0) {
      swap(nums, i, j)
      j++
    }
  }
}
function swap(nums, i, j) {
  let temp = nums[i]
  nums[i] = nums[j]
  nums[j] = temp
}

移动零-27

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

• 更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
• 返回 k。

用户评测：

评测机将使用以下代码测试您的解决方案：

int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
                            // 它以不等于 val 的值排序。

int k = removeElement(nums, val); // 调用你的实现

assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有的断言都通过，你的解决方案将会 通过。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3,_,_,_]
解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

链接

var removeElement = function (nums, val) {
  // 定义一个指针，指向不等于val元素的位置
  let k = 0

  for (let i = 0; i < nums.length; i++) {
    // 如果当前元素不等于val
    if (nums[i] !== val) {
      // 将不等于val的元素移动到前面
      nums[k] = nums[i]
      k++ // 移动指针到下一个位置
    }
  }

  // 返还不等于val的元素数量
  return k
}

删除有序数组中的重复项-26

给你一个 非严格递增排列 的数组 nums ，请你** 原地** 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

• 更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
• 返回 k 。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

链接

var removeDuplicates = function (nums) {
  // 如果数组为空，直接返回0
  if (nums.length === 0) return 0

  // 定义一个指针，指向唯一元素的位置
  let k = 1 // 从第二个元素开始

  for (let i = 1; i < nums.length; i++) {
    // 如果当前元素与前一个元素不同
    if (nums[i] !== nums[i - 1]) {
      // 将当前元素放到k指向的位置
      nums[k] = nums[i]
      k++
    }
  }

  // 返回唯一元素的数量
  return k
}

删除有序数组中的重复项 II -80

给你一个有序数组 nums ，请你** 原地** 删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

示例 1：

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,1,2,3,3]
输出：7, nums = [0,0,1,1,2,3,3]
解释：函数应返回新长度 length = 7, 并且原数组的前七个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。

链接

var removeDuplicates = function (nums) {
  // 如果数组为空，直接返回0
  if (nums.length === 0) return 0

  // 定义一个指针，指向不等于val元素的位置
  let k = 2 // 从第三个元素开始

  for (let i = 2; i < nums.length; i++) {
    // 如果当前元素与前两个元素不同
    if (nums[i] !== nums[k - 2]) {
      // 将当前元素放到k指向的位置
      nums[k] = nums[i]
      k++ // 移动指针到下一个位置
    }
  }

  // 返回新长度
  return k
}

颜色分类-75

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地 对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

示例 1：

输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

示例 2：

输入：nums = [2,0,1]
输出：[0,1,2]

链接

思路

计数排序

最简单的思路就是遍历一遍整个数组，统计出其中各个颜色的数量，最后把这个数组重新填充即可。

var sortColors = function (nums) {
  let colors = [0, 0, 0]
  for (let i = 0; i < nums.length; i++) {
    colors[nums[i]]++
  }
  nums.length = 0
  for (let i = 0; i < colors.length; i++) {
    for (let j = 0; j < colors[i]; j++) {
      nums.push(i)
    }
  }
}

三路快排

将整个数组分成三份，小于v，等于v和大于v。然后继续递归的对小于v和大于v进行三路快排

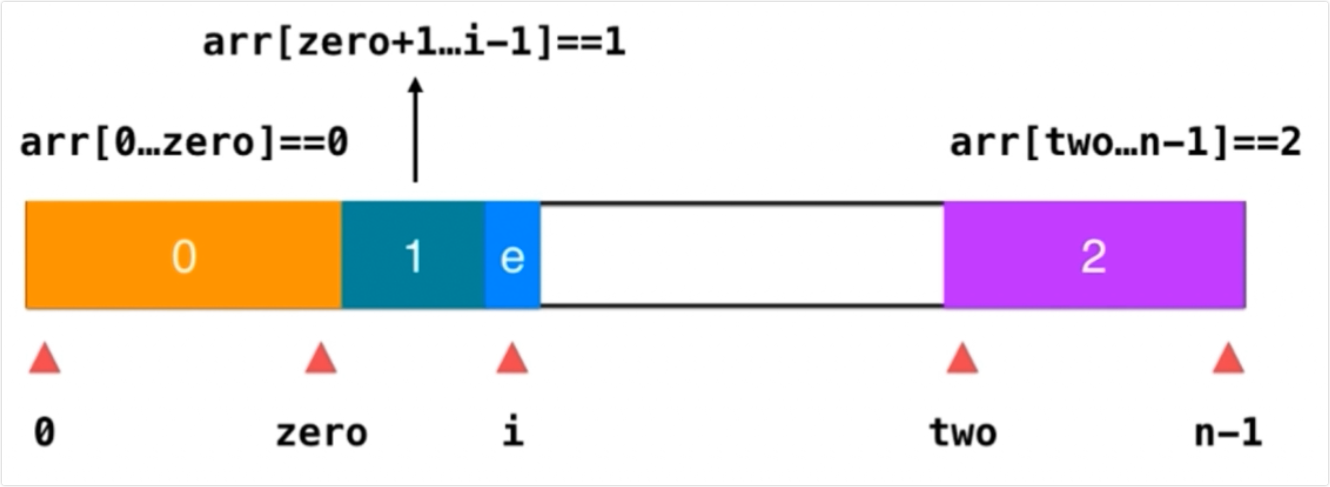
当遍历到当前e为1时，arr[zero+1...i-1]=1依然保持为1，i++

当e为2时，取出two前面一个元素和e交换位置，two--，i不动

当1为1时，e和arr[zero+1...i-1]第一个元素交换位置，i++

var sortColors = function (nums) {
  let zero = -1 // 小于1的区域的最后一个元素索引
  let two = nums.length // 大于1的区域的第一个元素索引
  let i = 0 // 当前遍历的元素索引

  while (i < two) {
    if (nums[i] === 0) {
      // 当前元素是0，交换到小于1的区域
      zero++
      ;[nums[zero], nums[i]] = [nums[i], nums[zero]]
      i++
    } else if (nums[i] === 2) {
      // 当前元素是2，交换到大于1的区域
      two--
      ;[nums[i], nums[two]] = [nums[two], nums[i]]
      // 注意：i不增加，因为交换后的nums[i]可能是0
    } else {
      // 当前元素时1，直接移动i
      i++
    }
  }
}

合并两个有序数组-88

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

**注意：**最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

链接

思路

从后往前的双指针思路，先定义指针 i 和 j 分别指向数组中有值的位置的末尾，再定义指针 k 指向待填充的数组 1 的末尾。

然后不断的迭代 i 和 j 指针，如果 i 位置的值比 j 大，就移动 i 位置的值到 k 位置，反之亦然。

如果 i 指针循环完了，j 指针的数组里还有值未处理的话，直接从 k 位置开始向前填充 j 指针数组即可。因为此时数组 1 原本的值一定全部被填充到了数组 1 的后面位置，且这些值一定全部大于此时 j 指针数组里的值。

var merge = function (nums1, m, nums2, n) {
  // 指向nums1和nums2的最后一个元素
  let i = m - 1 // nums1的最后一个有效元素索引
  let j = n - 1 // nums2的最后一个元素索引
  let k = m + n - 1 // 合并后数组的最后一个位置

  // 从后向前合并两个数组
  while (i >= 0 && j >= 0) {
    if (nums1[i] > nums2[j]) {
      nums1[k] = nums1[i] // 将nums1的元素放到合并后的数组中
      i--
    } else {
      nums1[k] = nums2[j] // 将nums2的元素放到合并后的数组中
      j--
    }
    k-- // 移动合并后数组的指针
  }

  // 如果nums2还有剩余元素，直接复制到nums1中
  while (j >= 0) {
    nums1[k] = nums2[j]
    j--
    k--
  }

  // 如果nums1还有剩余元素，不需要处理，因为它们已经在正确的位置
}

数组中的第K个最大元素-215

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

链接

思路

利用快排partition中，将pivot放置在了其正确的位置上的性质。

• quickSelect 函数接受左边界 left、右边界 right 和要查找的索引 indexToFind。

• 如果 left 等于 right，说明只有一个元素，直接返回该元素。

• 随机选择一个基准元素，并将其移到数组的末尾。

• 遍历数组，将大于基准的元素移到左边，并记录基准元素的最终位置。

• 根据基准元素的位置与目标索引的比较，决定在左边还是右边继续查找。

function findKthLargest(nums, k) {
  // 快速选择的分区函数
  function partition(left, right) {
    // 随机选择一个基准点，并与右边界交换
    const randomIndex = Math.floor(Math.random() * (right - left + 1)) + left
    ;[nums[randomIndex], nums[right]] = [nums[right], nums[randomIndex]]

    const pivot = nums[right] // 基准值
    let partitionIndex = left // 分区点

    for (let i = left; i < right; i++) {
      if (nums[i] > pivot) {
        // 降序排列
        ;[nums[i], nums[partitionIndex]] = [nums[partitionIndex], nums[i]]
        partitionIndex++
      }
    }
    // 将基准值放到正确位置
    ;[nums[partitionIndex], nums[right]] = [nums[right], nums[partitionIndex]]
    return partitionIndex
  }

  let left = 0,
    right = nums.length - 1
  const targetIndex = k - 1 // 第 k 大对应的索引

  while (left <= right) {
    const pivotIndex = partition(left, right)
    if (pivotIndex === targetIndex) {
      return nums[pivotIndex] // 找到目标元素
    } else if (pivotIndex < targetIndex) {
      left = pivotIndex + 1 // 在右侧搜索
    } else {
      right = pivotIndex - 1 // 在左侧搜索
    }
  }
}

hash表，空间换时间

var findKthLargest = function (nums, k) {
  // 找到数组中的最大元素
  let largest = -Infinity

  for (let i = 0; i < nums.length; i++) {
    if (nums[i] > largest) largest = nums[i]
  }

  // 构建一个哈希表，记录每个元素与最大值的差
  const hash = {}

  for (let i = 0; i < nums.length; i++) {
    const diff = largest - nums[i]
    hash[diff] = (hash[diff] || 0) + 1 // 记录差值出现的次数
  }

  // 找到第 k 大的元素
  let count = 0
  let diff = 0
  while (count < k) {
    count += hash[diff] || 0 // 累加当前差值的出现次数
    diff++
  }

  return largest - diff + 1 // 返回第 k 大的元素
}

两数之和 II - 输入有序数组-167

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

链接

思路

因为是有序数组，所以可以建立两个指针，i指向数组的头部，j指向数组的尾部。

此时开始遍历，如果左右指针指向的值，相加大于目标值，说明右指针需要左移指向稍小的值再尝试，反之左指针右移，如果相加的值相等，那么答案就是两个指针的值 [i, j]。

直到 i === j 循环终止。（对撞指针）

var twoSum = function (numbers, target) {
  let i = 0
  let j = numbers.length - 1
  while (i !== j) {
    let sum = numbers[i] + numbers[j]
    if (sum > target) {
      j--
    } else if (sum < target) {
      i++
    } else {
      return [i + 1, j + 1]
    }
  }
}

验证回文串-125

如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。

字母和数字都属于字母数字字符。

给你一个字符串 s，如果它是 回文串 ，返回 true ；否则，返回 false 。

示例 1：

输入: s = "A man, a plan, a canal: Panama"
输出：true
解释："amanaplanacanalpanama" 是回文串。

示例 2：

输入：s = "race a car"
输出：false
解释："raceacar" 不是回文串。

示例 3：

输入：s = " "
输出：true
解释：在移除非字母数字字符之后，s 是一个空字符串 "" 。
由于空字符串正着反着读都一样，所以是回文串。

链接

思路

先根据题目给出的条件，通过正则把不匹配字符去掉，然后转小写。

建立双指针 i, j 分别指向头和尾，然后两个指针不断的向中间靠近，每前进一步就对比两端的字符串是否相等，如果不相等则直接返回 false。

如果直到 i >= j 也就是指针对撞了，都没有返回 false，那就说明符合「回文」的定义，返回 true。

/**
 * @param {string} s
 * @return {boolean}
 */
var isPalindrome = function (s) {
  s = s.replace(/[^0-9a-zA-Z]/g, '').toLowerCase()
  let i = 0
  let j = s.length - 1

  while (i < j) {
    let head = s[i]
    let tail = s[j]

    if (head !== tail) {
      return false
    } else {
      i++
      j--
    }
  }
  return true
}

反转字符串-344

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。

示例 1：

输入：s = ["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：s = ["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

链接

思路

双指针法：使用两个指针 left 和 right，分别指向数组的开始和结束。通过交换这两个指针指向的字符来反转数组。

/**
 * @param {character[]} s
 * @return {void} Do not return anything, modify s in-place instead.
 */
var reverseString = function (s) {
  let i = 0
  let j = s.length - 1

  while (i < j) {
    ;[s[i], s[j]] = [s[j], s[i]]
    i++
    j--
  }
  return s
}

12.反转字符串中的元音字母-345

给你一个字符串 s ，仅反转字符串中的所有元音字母，并返回结果字符串。

元音字母包括 'a'、'e'、'i'、'o'、'u'，且可能以大小写两种形式出现不止一次。

示例 1：

**输入：**s = "IceCreAm"

输出："AceCreIm"

解释：

s 中的元音是 ['I', 'e', 'e', 'A']。反转这些元音，s 变为 "AceCreIm".

示例 2：

**输入：**s = "leetcode"

输出："leotcede"

链接

/**
 * 反转字符串中的所有元音字母
 * @param {string} s - 输入字符串
 * @return {string} - 反转元音后的字符串
 */
var reverseVowels = function (s) {
  const vowels = 'aeiouAEIOU' // 定义元音字母
  const sArray = s.split('') // 将字符串转换为字符数组
  let left = 0 // 左指针
  let right = sArray.length - 1 // 右指针

  // 使用双指针反转元音字母
  while (left < right) {
    // 找到左侧的元音字母
    while (left < right && !vowels.includes(sArray[left])) {
      left++ // 移动左指针
    }
    // 找到右侧的元音字母
    while (left < right && !vowels.includes(sArray[right])) {
      right-- // 移动右指针
    }
    // 交换元音字母
    if (left < right) {
      ;[sArray[left], sArray[right]] = [sArray[right], sArray[left]]
      left++ // 移动左指针
      right-- // 移动右指针
    }
  }

  return sArray.join('') // 将字符数组转换回字符串并返回
}

盛最多水的容器-11

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

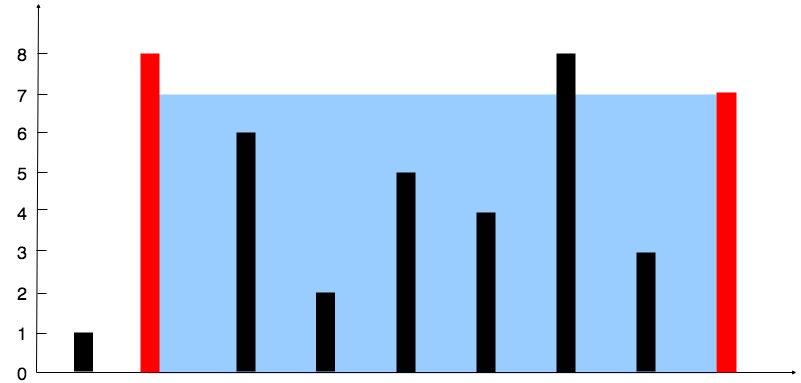
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

思路

这题利用双指针去做，i 指向最左边，j 指向最右边。当发现左边比较高的时候，保持左边 不动，右边左移。当发现右边比较高的时候，保持右边不动，左边右移。在这个过程中不断 更新最大值，最后 i === j 的时候，即可求得最大值。

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function (height) {
  let i = 0
  let j = height.length - 1

  let max = 0

  while (i !== j) {
    let leftHeight = height[i]
    let rightHeight = height[j]

    let x = j - i
    let area
    if (leftHeight > rightHeight) {
      area = rightHeight * x
      j--
    } else {
      area = leftHeight * x
      i++
    }
    max = area > max ? area : max
  }

  return max
}

长度最小的子数组-209

给定一个含有 n 个正整数的数组和一个正整数 target **。找出该数组中满足其总和大于等于 target 的长度最小的 子数组[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

链接

思路

暴力法（优化）

纯暴力的循环也就是穷举每种子数组并求和，当然是会超时的，这里就不做讲解了。下面这种解法会在暴力法的基础上稍作优化，具体的思路如下：

1. 先选定下标 i 从 0 作为切分数组的起点，然后下标 j 作为数组的右边界从 0 开始不停向后扩展，每往后一位，就把本次的求和加上新的数字，只要本轮循环的和大于 s，就应该停止循环，因为没必要再往后扩展了，往后扩展的数组长度一定是大于当前长度的。
2. 选定下标 1 为切分数组的起点，进入下一轮循环。

/**
 * @param {number} target
 * @param {number[]} nums
 * @return {number}
 */
var minSubArrayLen = function (target, nums) {
  let min = Infinity
  for (let i = 0; i < nums.length; i++) {
    let sum = 0
    for (let j = i; j < nums.length; j++) {
      sum += nums[j]
      if (sum >= target) {
        min = Math.min(min, j - i + 1)
        if (min === 1) {
          return min
        }
        break
      }
    }
  }
  return min === Infinity ? 0 : min
}

滑动窗口

定义两个下标 i、j 为左右边界，中间的子数组为滑动窗口。在更新窗口的过程中不断的更新窗口之间的值的和 sum。

1. 当 sum < 目标值，说明值不够大，j++，右边界右移。
2. 当 sum >= 目标值，满足条件，把当前窗口的大小和记录的最小值进行对比，更新最小值。并且 i++ 左窗口右移，继续找最优解。

当 i 超出了数组的右边界，循环终止。

/**
 * @param {number} target
 * @param {number[]} nums
 * @return {number}
 */
var minSubArrayLen = function (target, nums) {
  let n = nums.length
  // 定义[i,...]滚动窗口，取这个窗口里的和
  let i = 0
  let j = -1

  let sum = 0
  let res = Infinity

  while (i < n) {
    if (sum < target) {
      sum += nums[++j]
    } else {
      sum -= nums[i++]
    }

    if (sum >= target) {
      res = Math.min(res, j - i + 1)
    }
  }

  return res === Infinity ? 0 : res
}

15.无重复字符的最长子串-3

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

链接

思路

这题是比较典型的滑动窗口问题，定义一个左边界 left 和一个右边界 right，形成一个窗口，并且在这个窗口中保证不出现重复的字符串。

这需要用到一个新的变量 freqMap，用来记录窗口中的字母出现的频率数。在此基础上，先尝试取窗口的右边界再右边一个位置的值，也就是 str[right + 1]，然后拿这个值去 freqMap 中查找：

1. 这个值没有出现过，那就直接把 right ++，扩大窗口右边界。
2. 如果这个值出现过，那么把 left ++，缩进左边界，并且记得把 str[left] 位置的值在 freqMap 中减掉。

循环条件是 left < str.length，允许左边界一直滑动到字符串的右界。

/**
 * @param {string} s
 * @return {number}
 */
let lengthOfLongestSubstring = function (s) {
  let n = s.length
  // 滑动窗口为s[left...right]
  let left = 0
  let right = -1
  let freqMap = {} // 记录当前子串中下标对应的出现频率
  let max = 0 // 找到的满足条件子串的最长长度

  while (left < n) {
    let nextLetter = s[right + 1]
    if (!freqMap[nextLetter] && nextLetter !== undefined) {
      freqMap[nextLetter] = 1
      right++
    } else {
      freqMap[s[left]] = 0
      left++
    }
    max = Math.max(max, right - left + 1)
  }

  return max
}

找到字符串中所有字母异位词-438

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

示例 1:

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

示例 2:

输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

思路

还是典型的滑动窗口去解决的问题，由于字母异位词一定是长度相等的，所以我们需要把窗口的长度始终维持在目标字符的长度，也就是说，每次循环结束后 left 和 right 是同步前进的。

由于字母异位词不需要考虑顺序，所以只需要运用一个辅助函数 isAnagrams 去判断两个 map 中记录的字母次数，即可判断出当前位置开始的子串是否和目标字符串形成字母异位词。

/**
 * @param {string} s
 * @param {string} p
 * @return {number[]}
 */
var findAnagrams = function (s, p) {
  let targetMap = makeCountMap(p)
  let sL = s.length
  let pL = p.length
  // [left...right]滑动窗口
  let left = 0
  let right = pL - 1
  let windowMap = makeCountMap(s.substring(left, right + 1))
  let res = []

  while (left <= sL - pL && right < sL) {
    if (isAnagrams(windowMap, targetMap)) {
      res.push(left)
    }
    windowMap[s[left]]--
    right++
    left++
    addCountToMap(windowMap, s[right])
  }

  return res
}

function isAnagrams(windowMap, targetMap) {
  let targetKeys = Object.keys(targetMap)
  for (let targetKey of targetKeys) {
    if (
      !windowMap[targetKey] ||
      windowMap[targetKey] !== targetMap[targetKey]
    ) {
      return false
    }
  }
  return true
}

function addCountToMap(map, str) {
  if (!map[str]) {
    map[str] = 1
  } else {
    map[str]++
  }
}

function makeCountMap(strs) {
  let map = {}
  for (let i = 0; i < strs.length; i++) {
    let letter = strs[i]
    addCountToMap(map, letter)
  }
  return map
}

最小覆盖子串-76

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字符的最小子串。

示例：

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"

说明：

如果 S 中不存这样的子串，则返回空字符串 ""。 如果 S 中存在这样的子串，我们保证它是唯一的答案。

leetcode-cn.com/problems/minimum-window-substring

思路

根据目标字符串 t生成一个目标 map，记录每个字符的目标值出现的次数。
然后就是维护一个滑动窗口，并且针对这个滑动窗口中的字符也生成一个 map 去记录字符出现次数。

每次循环都去对比窗口的 map 里的字符是否能覆盖目标 map 里的字符。

覆盖的意思就是，目标 map 里的每个字符在窗口 map 中出现，并且出现的次数要 >= 目标 map 中此字符出现的次数。

窗口滑动逻辑：
1.如果当前还没有能覆盖，那么就右滑右边界。
2.如果当前已经覆盖了，记录下当前的子串，并且右滑左边界看看能否进一步缩小子串的长度。

两种情况下停止循环，返回结果：
1.左边界达到 给定字符长度 - 目标字符的长度，此时不管匹配与否，都是最短能满足的了。
2.右边界超出给定字符的长度，这种情况会出现在右边界已经到头了，但是还没有能覆盖目标字符串，此时就算继续滑动也不可能得到结果了。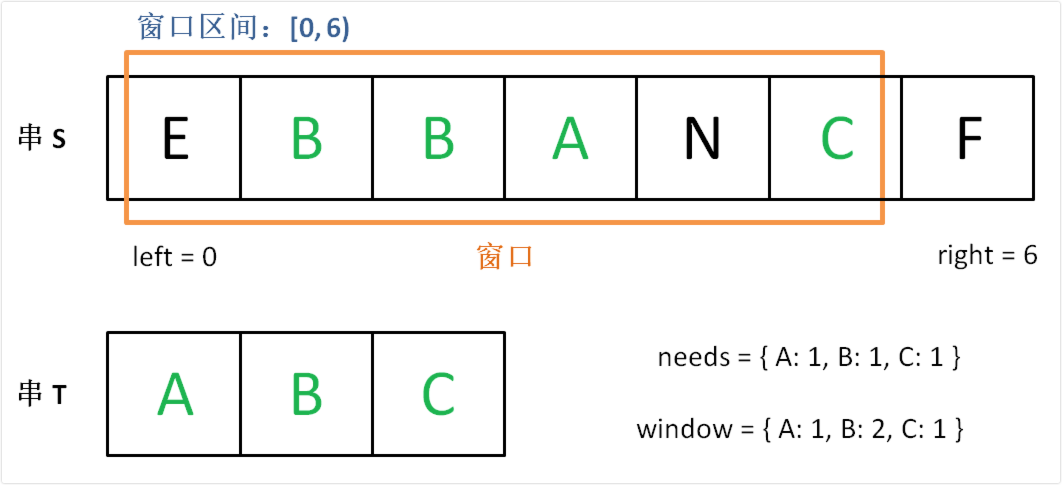

/**
 * @param {string} s
 * @param {string} t
 * @return {string}
 */
let minWindow = function (s, t) {
  // 先制定目标 根据t字符串统计出每个字符应该出现的个数
  let targetMap = makeCountMap(t)

  let sl = s.length
  let tl = t.length
  let left = 0 // 左边界
  let right = -1 // 右边界
  let countMap = {} // 当前窗口子串中 每个字符出现的次数
  let min = '' // 当前计算出的最小子串

  // 循环终止条件是两者有一者超出边界
  while (left <= sl - tl && right <= sl) {
    // 和 targetMap 对比出现次数 确定是否满足条件
    let isValid = true
    Object.keys(targetMap).forEach((key) => {
      let targetCount = targetMap[key]
      let count = countMap[key]
      if (!count || count < targetCount) {
        isValid = false
      }
    })

    if (isValid) {
      // 如果满足 记录当前的子串 并且左边界右移
      let currentValidLength = right - left + 1
      if (currentValidLength < min.length || min === '') {
        min = s.substring(left, right + 1)
      }
      // 也要把map里对应的项去掉
      countMap[s[left]]--
      left++
    } else {
      // 否则右边界右移
      addCountToMap(countMap, s[right + 1])
      right++
    }
  }

  return min
}

function addCountToMap(map, str) {
  if (!map[str]) {
    map[str] = 1
  } else {
    map[str]++
  }
}

function makeCountMap(strs) {
  let map = {}
  for (let i = 0; i < strs.length; i++) {
    let letter = strs[i]
    addCountToMap(map, letter)
  }
  return map
}

两个数组的交集-349

给定两个数组 nums1 和 nums2 ，返回 它们的 交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

链接

思路：

使用两个集合来存储 nums1 和 nums2 中的元素，这样可以自动去重。

然后使用集合的交集操作来找到两个集合的共同元素。

最后将交集转换为数组并返回。

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number[]}
 */
var intersection = function (nums1, nums2) {
  // 使用 Set 去重并存储 nums1 和 nums2 的元素
  const set1 = new Set(nums1)
  const set2 = new Set(nums2)

  // 使用 Array.from() 和 filter() 找到交集
  const result = Array.from(set1).filter((num) => set2.has(num))

  return result
}

两个数组的交集 II-350

给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

示例 2:

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]

链接

思路

为两个数组分别建立 map，用来存储 num -> count 的键值对，统计每个数字出现的数量。

然后对其中一个 map 进行遍历，查看这个数字在两个数组中分别出现的数量，取出现的最小的那个数量（比如数组 1 中出现了 1 次，数组 2 中出现了 2 次，那么交集应该取 1 次），push 到结果数组中即可。

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number[]}
 */
var intersect = function (nums1, nums2) {
  let map1 = makeCountMap(nums1)
  let map2 = makeCountMap(nums2)
  let res = []
  for (let num of map1.keys()) {
    const count1 = map1.get(num)
    const count2 = map2.get(num)

    if (count2) {
      const pushCount = Math.min(count1, count2)
      for (let i = 0; i < pushCount; i++) {
        res.push(num)
      }
    }
  }
  return res
}

function makeCountMap(nums) {
  let map = new Map()
  for (let i = 0; i < nums.length; i++) {
    let num = nums[i]
    let count = map.get(num)
    if (count) {
      map.set(num, count + 1)
    } else {
      map.set(num, 1)
    }
  }
  return map
}

进阶

1. 排好序的数组。 对于排好序的数组，用双指针的方法会更优。
2. 两个数组数量差距很大。 优先遍历容量小的数组，提前结束循环。

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number[]}
 */
var intersectSorted = function (nums1, nums2) {
  const result = []
  let i = 0,
    j = 0

  while (i < nums1.length && j < nums2.length) {
    if (nums1[i] < nums2[j]) {
      i++
    } else if (nums1[i] > nums2[j]) {
      j++
    } else {
      result.push(nums1[i])
      i++
      j++
    }
  }

  return result // 返回交集数组
}

// 示例用法
console.log(intersectSorted([1, 2, 2, 3], [2, 2, 3, 4])) // 输出: [2, 2, 3]

有效的字母异位词-242

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词

示例 1:

输入: s = "anagram", t = "nagaram"
输出: true

示例 2:

输入: s = "rat", t = "car"
输出: false

链接

思路

1. 如果两个字符串的长度不同，则 t 不可能是 s 的字母异位词，直接返回 false。
2. 使用一个对象或数组来记录 s 中每个字符的出现次数。
3. 遍历 t，对于每个字符，减少计数。如果某个字符的计数变为负数，说明 t 中的字符超出了 s 中的字符，返回 false。
4. 最后检查计数对象或数组中所有字符的计数是否为零，如果是，则返回 true，否则返回 false。

/**
 * @param {string} s
 * @param {string} t
 * @return {boolean}
 */
var isAnagram = function (s, t) {
  // 如果长度不同，直接返回
  if (s.length !== t.length) {
    return false
  }
  const countMap = {}

  // 记录s中每个字符的出现次数
  for (let char of s) {
    countMap[char] = (countMap[char] || 0) + 1
  }

  // 遍历t，减少计数
  for (let char of t) {
    if (!countMap[char]) {
      return false // 如果字符不存在或计数为0，返回
    }
    countMap[char]--
  }

  // 检查所有字符的计数是否为0
  return Object.values(countMap).every((count) => count === 0)
}

快乐数-202

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

示例 2：

输入：n = 2
输出：false

链接

思路：

1. 创建一个函数来计算一个数字的每个位置上的数字的平方和。
2. 使用一个集合来存储已经出现过的数字。
3. 在循环中，不断计算平方和并检查是否为 1 或者是否已经在集合中出现过。
4. 如果结果为 1，返回 true；如果出现重复，返回 false。

/**
 * @param {number} n
 * @return {boolean}
 */
var isHappy = function (n) {
  const seen = new Set()

  while (n !== 1) {
    if (seen.has(n)) {
      return false // 如果出现重复，返回false
    }
    seen.add(n)
    n = getNext(n) // 计算下一个数字
  }

  return true // 如果最终结果为1，返回true
}

// 计算数字每个位置上的数字的平方和
function getNext(num) {
  let totalSum = 0
  while (num > 0) {
    const digit = num % 10 // 获取最后一位数字
    totalSum += digit * digit // 计算平方
    num = Math.floor(num / 10) // 去掉最后一位数字
  }
  return totalSum
}

单词规律-290

给定一种规律 pattern 和一个字符串 s ，判断 s 是否遵循相同的规律。

这里的 遵循 指完全匹配，例如， pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。

示例1:

输入: pattern = "abba", s = "dog cat cat dog"
输出: true

示例 2:

输入:pattern = "abba", s = "dog cat cat fish"
输出: false

示例 3:

输入: pattern = "aaaa", s = "dog cat cat dog"
输出: false

链接

思路

要判断 pattern 是否与字符串 s 具有相同的规律，我们需要检查两个条件：

1. pattern 中的每个字符映射到字符串 s 中的一个唯一单词。
2. s 中的每个单词映射到 pattern 中的一个唯一字符。

这是一个双射映射的问题，可以使用两张哈希表或一个哈希表和一个集合来实现映射关系的验证。

/**
 * @param {string} pattern
 * @param {string} s
 * @return {boolean}
 */
var wordPattern = function (pattern, s) {
  const words = s.split(' ') // 按空格分割字符串
  if (pattern.length !== words.length) return false // 长度不匹配直接返回 false

  const charToWord = new Map() // 存储字符到单词的映射
  const usedWords = new Set() // 存储已经映射过的单词

  for (let i = 0; i < pattern.length; i++) {
    const char = pattern[i]
    const word = words[i]

    if (charToWord.has(char)) {
      // 如果字符已存在映射，检查是否匹配
      if (charToWord.get(char) !== word) return false
    } else {
      // 如果字符无映射，检查单词是否已被使用
      if (usedWords.has(word)) return false
      // 建立新映射
      charToWord.set(char, word)
      usedWords.add(word)
    }
  }

  return true // 如果遍历结束未发现矛盾，返回 true
}

同构字符串-205

给定两个字符串 s 和 t ，判断它们是否是同构的。

如果 s 中的字符可以按某种映射关系替换得到 t ，那么这两个字符串是同构的。

每个出现的字符都应当映射到另一个字符，同时不改变字符的顺序。不同字符不能映射到同一个字符上，相同字符只能映射到同一个字符上，字符可以映射到自己本身。

示例 1:

输入：s = "egg", t = "add"
输出：true

示例 2：

输入：s = "foo", t = "bar"
输出：false

示例 3：

输入：s = "paper", t = "title"
输出：true

链接

思路

要判断两个字符串是否是同构字符串，我们需要检查以下条件：

1. 一对一映射关系：
   • 字符串 s 中的每个字符必须唯一映射到字符串 t 中的字符。
   • 字符串 t 中的每个字符也必须唯一映射到字符串 s 中的字符。
2. 双向映射：
   • 使用两个哈希表（或 Map）来记录：
     • s 中的字符到 t 中的字符的映射。
     • t 中的字符到 s 中的字符的映射。
3. 遍历验证：
   • 如果发现映射冲突，即同一个字符映射到不同字符，或不同字符映射到同一个字符，则返回 false。

/**
 * @param {string} s
 * @param {string} t
 * @return {boolean}
 */
var isIsomorphic = function (s, t) {
  if (s.length !== t.length) return false // 长度不同直接返回false

  const mapS = new Map() // s到t的映射
  const mapT = new Map() // t到s的映射

  for (let i = 0; i < s.length; i++) {
    const charS = s[i]
    const chatT = t[i]

    // 检查 s->t 的映射是否一致
    if (mapS.has(charS) && mapS.get(charS) !== chatT) return false

    // 检查 t->s 的映射是否一致
    if (mapT.has(chatT) && mapT.get(chatT) !== charS) return false

    // 建立映射
    mapS.set(charS, chatT)
    mapT.set(chatT, charS)
  }

  return true // 未发现矛盾，返回true
}

根据字符出现频率排序-451

给定一个字符串 s ，根据字符出现的 频率 对其进行 降序排序 。一个字符出现的 频率 是它出现在字符串中的次数。

返回 已排序的字符串 。如果有多个答案，返回其中任何一个。

示例 1:

输入: s = "tree"
输出: "eert"
解释: 'e'出现两次，'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外，"eetr"也是一个有效的答案。

示例 2:

输入: s = "cccaaa"
输出: "cccaaa"
解释: 'c'和'a'都出现三次。此外，"aaaccc"也是有效的答案。
注意"cacaca"是不正确的，因为相同的字母必须放在一起。

示例 3:

输入: s = "Aabb"
输出: "bbAa"
解释: 此外，"bbaA"也是一个有效的答案，但"Aabb"是不正确的。
注意'A'和'a'被认为是两种不同的字符。

链接

思路

要根据字符的出现频率对字符串进行降序排序，可以按照以下步骤实现：

1. 统计频率：
   • 使用哈希表（Map）存储每个字符及其出现次数。
2. 排序字符：
   • 将哈希表中的字符及其频率转化为数组。
   • 根据频率进行降序排序。
3. 重构字符串：
   • 遍历排序后的数组，根据每个字符的频率生成对应的子串，并拼接成最终结果。

/**
 * @param {string} s
 * @return {string}
 */
var frequencySort = function (s) {
  const freqMap = new Map()

  // 统计字符出现的次数
  for (const char of s) {
    freqMap.set(char, (freqMap.get(char) || 0) + 1)
  }

  // 根据次数排序
  const sortedChars = Array.from(freqMap.entries()).sort((a, b) => b[1] - a[1])

  // 根据次数重构字符串
  let result = ''
  for (const [char, freq] of sortedChars) {
    result += char.repeat(freq)
  }

  return result
}

两数之和-1

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

链接

思路

我们可以通过以下步骤来解决这个问题：

1. 哈希表辅助：
   • 使用一个哈希表存储数组中的每个元素的值及其对应的索引。
   • 在遍历数组时，检查当前数的“目标差值”是否已经存在于哈希表中。
   • 如果存在，说明我们找到了两个数，它们的和等于目标值，可以直接返回它们的索引。
   • 如果不存在，将当前元素添加到哈希表中。
2. 优化时间复杂度：
   • 使用哈希表可以将查找的时间复杂度降为 O(1)，从而使整体时间复杂度为 O(n)。

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var twoSum = function (nums, target) {
  const map = new Map() // 哈希表用于存储值和索引的映射

  for (let i = 0; i < nums.length; i++) {
    const diff = target - nums[i] // 计算目标差值

    // 如果差值已存于哈希表中，直接返回
    if (map.has(diff)) {
      return [map.get(diff), i]
    }

    // 否则将当前值和索引存入哈希表
    map.set(nums[i], i)
  }

  // 理论上不会执行到这里，因为题目保证一定有值
  return []
}

三数之和-15

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

链接

思路

我们可以通过排序 + 双指针的方法高效解决该问题：

1. 排序数组：
   • 首先将数组 nums 从小到大排序。
   • 排序的目的是方便我们在后续处理中避免重复的三元组，以及使用双指针快速寻找满足条件的元素。
2. 固定一个数，寻找剩余两个数：
   • 遍历数组，固定当前数字 nums[i]，将问题转化为在剩余数组中寻找两个数，使它们的和等于 -nums[i]。
   • 利用双指针在排序数组中高效地找到这两个数。
3. 避免重复：
   • 对固定的数字 nums[i]，如果它与前一个数字相同，则跳过，避免产生重复的三元组。
   • 在双指针移动过程中，也需要跳过相同的数字以避免重复。
4. 双指针的操作：
   • 左指针 left 指向当前数字之后的位置，右指针 right 指向数组末尾。
   • 计算三数之和：
     • 如果和为 0，记录结果，并移动两个指针以继续查找其他可能的组合。
     • 如果和小于 0，说明左指针的数字偏小，右移左指针。
     • 如果和大于 0，说明右指针的数字偏大，左移右指针。

/**
 * 找到所有和为 0 的三元组
 * @param {number[]} nums - 输入整数数组
 * @return {number[][]} - 所有不重复的三元组
 */
var threeSum = function (nums) {
  const result = []
  const n = nums.length

  // 1. 排序数组
  nums.sort((a, b) => a - b)

  // 2. 遍历数组，固定一个数
  for (let i = 0; i < n - 2; i++) {
    // 跳过重复的数字
    if (i > 0 && nums[i] === nums[i - 1]) continue

    let left = i + 1,
      right = n - 1

    // 3. 双指针寻找满足条件的二元组
    while (left < right) {
      const sum = nums[i] + nums[left] + nums[right]
      if (sum === 0) {
        result.push([nums[i], nums[left], nums[right]])

        // 跳过重复的左指针数字
        while (left < right && nums[left] === nums[left + 1]) left++
        // 跳过重复的右指针数字
        while (left < right && nums[right] === nums[right - 1]) right--

        // 移动双指针
        left++
        right--
      } else if (sum < 0) {
        left++
      } else {
        right--
      }
    }
  }

  return result
}

四数之和-18

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案 。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

链接

思路

四数之和问题可以通过排序 + 双指针的方法进行优化解决。与三数之和类似，使用双层循环固定两个数，利用双指针寻找剩余的两个数。

具体步骤：

1. 数组排序：
   • 对 nums 进行从小到大的排序，方便后续处理重复问题和双指针操作。
2. 固定两个数，寻找另外两个数：
   • 使用两层循环分别固定 nums[i] 和 nums[j]，将问题转化为在剩余数组中寻找两个数，使它们的和等于 target - nums[i] - nums[j]。
3. 双指针查找：
   • 左指针从固定数的右侧开始，右指针从数组末尾开始。
   • 计算四数之和：
     • 如果等于目标值，则记录结果，并移动双指针以查找其他可能的组合。
     • 如果和小于目标值，左指针右移。
     • 如果和大于目标值，右指针左移。
4. 避免重复：
   • 对固定的两个数字以及双指针的结果都需要进行去重。

/**
 * 找到所有和为 target 的四元组
 * @param {number[]} nums - 输入数组
 * @param {number} target - 目标值
 * @return {number[][]} - 所有不重复的四元组
 */
var fourSum = function (nums, target) {
  const result = []
  const n = nums.length

  // 1. 排序数组
  nums.sort((a, b) => a - b)

  // 2. 第一层循环固定第一个数
  for (let i = 0; i < n - 3; i++) {
    if (i > 0 && nums[i] === nums[i - 1]) continue // 跳过重复的第一个数

    // 3. 第二层循环固定第二个数
    for (let j = i + 1; j < n - 2; j++) {
      if (j > i + 1 && nums[j] === nums[j - 1]) continue // 跳过重复的第二个数

      let left = j + 1,
        right = n - 1

      // 4. 双指针寻找另外两个数
      while (left < right) {
        const sum = nums[i] + nums[j] + nums[left] + nums[right]

        if (sum === target) {
          result.push([nums[i], nums[j], nums[left], nums[right]])

          // 跳过重复的左指针和右指针
          while (left < right && nums[left] === nums[left + 1]) left++
          while (left < right && nums[right] === nums[right - 1]) right--

          left++
          right--
        } else if (sum < target) {
          left++ // 和小于目标值，左指针右移
        } else {
          right-- // 和大于目标值，右指针左移
        }
      }
    }
  }

  return result
}

最接近的三数之和-16

给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

示例：
输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

提示：

3 <= nums.length <= 10^3
-10^3 <= nums[i] <= 10^3
-10^4 <= target <= 10^4

leetcode-cn.com/problems/3sum-closest

思路

先按照升序排序，然后分别从左往右依次选择一个基础点 i（0 <= i <= nums.length - 3），在基础点的右侧用双指针去不断的找最小的差值。

假设基础点是 i，初始化的时候，双指针分别是：

• left：i + 1，基础点右边一位。
• right: nums.length - 1 数组最后一位。

然后求此时的和，如果和大于 target，那么可以把右指针左移一位，去试试更小一点的值，反之则把左指针右移。

在这个过程中，不断更新全局的最小差值 min，和此时记录下来的和 res。

最后返回 res 即可。

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var threeSumClosest = function (nums, target) {
  let n = nums.length
  if (n === 3) {
    return getSum(nums)
  }

  // 先升序排序，此为解题前置条件
  nums.sort((a, b) => a - b)

  let min = Infinity // 和target的最小差
  let res

  // 从左往右依次尝试定一个基础指针，右边至少再保留两位，否则无法凑成3个
  for (let i = 0; i <= n - 3; i++) {
    let basic = nums[i]
    let left = i + 1 // 左指针先从 i 右侧的第一为开始尝试
    let right = n - 1 // 右指针先从数组最后一项开始尝试

    while (left < right) {
      let sum = basic + nums[left] + nums[right] // 三数求和
      // 更新最小差
      let diff = Math.abs(sum - target)
      if (diff < min) {
        min = diff
        res = sum
      }
      if (sum < target) {
        // 求出的和如果小于目标值的话，可以尝试把左指针右移扩大值
        left++
      } else if (sum > target) {
        // 反之则右指针左移
        right--
      } else {
        // 相等的话，差就为0，一定是答案
        return sum
      }
    }
  }

  return res
}

function getSum(nums) {
  return nums.reduce((total, cur) => total + cur, 0)
}

四数相加 II-454

给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：

• 0 <= i, j, k, l < n
• nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0

示例 1：

输入：nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出：2
解释：
两个元组如下：
1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0

示例 2：

输入：nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出：1

链接

思路

1. 分组并哈希存储

将四个数组分成两组：

• 对于 nums1 和 nums2 的任意两数之和，存入哈希表，键为两数之和，值为该和出现的次数。
• 对于 nums3 和 nums4 的任意两数之和，判断其相反数是否存在于哈希表中。

2. 利用哈希表查找匹配

• 在第二组中，逐一计算 nums3[k] + nums4[l] 的相反数 -(nums3[k] + nums4[l])。
• 如果该相反数存在于哈希表，则表明找到了若干对符合条件的四元组，其数量等于哈希表中对应的值。

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @param {number[]} nums3
 * @param {number[]} nums4
 * @return {number}
 */
var fourSumCount = function (nums1, nums2, nums3, nums4) {
  const map = new Map()

  // 1.计算nums1 和 nums2的两数之和，并存入哈希表
  for (let a of nums1) {
    for (let b of nums2) {
      const sum = a + b
      map.set(sum, (map.get(sum) || 0) + 1)
    }
  }

  let count = 0

  // 2.计算nums3 和 nums4 的两数之和，并查找其相反数是否在哈希表中
  for (let c of nums3) {
    for (let d of nums4) {
      const complement = -[c + d]
      if (map.has(complement)) {
        count += map.get(complement)
      }
    }
  }

  return count
}

字母异位词分组-49

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

示例 2:

输入: strs = [""]
输出: [[""]]

示例 3:

输入: strs = ["a"]
输出: [["a"]]

链接

思路

1. 排序字符串分组：
   • 对字符串数组中的每个字符串，按字母排序，将排序后的字符串作为键存入哈希表。
   • 哈希表的值是具有相同排序结果的字符串列表。
2. 返回分组结果：
   • 最后，将哈希表的值转为结果数组。

/**
 * @param {string[]} strs
 * @return {string[][]}
 */
var groupAnagrams = function (strs) {
  const map = new Map()

  for (let str of strs) {
    // 对字符串排序，作为哈希表的键
    const sortedStr = str.split('').sort().join('')
    if (!map.has(sortedStr)) {
      map.set(sortedStr, [])
    }
    map.get(sortedStr).push(str)
  }

  // 返回哈希表的值，即分组结果
  return Array.from(map.values())
}

回旋镖的数量-447

给定平面上 n 对 互不相同 的点 points ，其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ，其中 i 和 j 之间的欧式距离和 i 和 k 之间的欧式距离相等（需要考虑元组的顺序）。

返回平面上所有回旋镖的数量。

示例 1：

输入：points = [[0,0],[1,0],[2,0]]
输出：2
解释：两个回旋镖为 [[1,0],[0,0],[2,0]] 和 [[1,0],[2,0],[0,0]]

示例 2：

输入：points = [[1,1],[2,2],[3,3]]
输出：2

示例 3：

输入：points = [[1,1]]
输出：0

链接

思路

1. 核心思想：
   • 对每个点 i，计算它到其他点的欧式距离的平方（避免浮点运算）。
   • 用哈希表记录距离出现的次数。如果某个距离出现了 n 次，则这些点与 i 可以构成 n×(n−1) 个回旋镖。
2. 步骤：
   • 遍历每个点 i。
   • 对于点 i，计算到其他点的距离平方，用哈希表记录频次。
   • 遍历哈希表，根据公式 n×(n−1) 累加回旋镖数量。
3. 优化：
   • 欧式距离平方的计算避免浮点数运算。
   • 哈希表在每次处理完点 i 后清空。

/**
 * @param {number[][]} points
 * @return {number}
 */
var numberOfBoomerangs = function (points) {
  let result = 0

  for (let i = 0; i < points.length; i++) {
    const distanceMap = new Map()

    for (let j = 0; j < points.length; j++) {
      if (i === j) continue

      // 计算点i和点j的距离平方
      const dx = points[i][0] - points[j][0]
      const dy = points[i][1] - points[j][1]
      const distanceSquared = dx * dx + dy * dy

      // 更新哈希表中的频次
      distanceMap.set(
        distanceSquared,
        (distanceMap.get(distanceSquared) || 0) + 1
      )
    }

    // 遍历哈希表，计算回旋标数量
    for (const count of distanceMap.values()) {
      if (count > 1) {
        result += count * (count - 1)
      }
    }
  }

  return result
}

直线上最多的点数-149

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

示例 1：

输入：points = [[1,1],[2,2],[3,3]]
输出：3

示例 2：

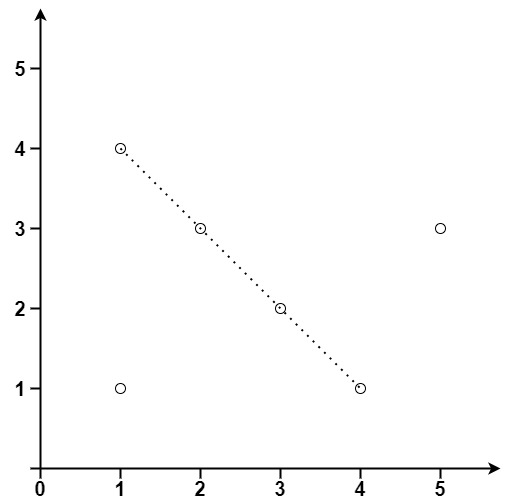
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

链接

/**
 * @param {number[][]} points
 * @return {number}
 */
var maxPoints = function (points) {
  // 边界情况
  if (points.length <= 2) {
    return points.length
  }

  let maxCount = 0

  // 遍历每一个点作为起点
  for (let i = 0; i < points.length; i++) {
    const slopes = new Map()
    let duplicate = 1 // 用于统计重复点

    for (let j = i + 1; j < points.length; j++) {
      // 处理重复点
      if (points[i][0] === points[j][0] && points[i][1] === points[j][1]) {
        duplicate++
        continue
      }

      // 计算斜率（dy/dx）
      let dx = points[j][0] - points[i][0]
      let dy = points[j][1] - points[i][1]

      // 处理斜率无穷大的情况（垂直线）
      if (dx === 0) {
        dy = 1 // 设置为无穷大
      } else if (dy === 0) {
        dx = 1 // 水平线的斜率为0
      } else {
        // 计算斜率的最高形式（dy/dx）
        const g = gcd(dy, dx)
        dy /= g
        dx /= g
      }

      // 使用斜率作为哈希表的键
      const slope = `${dy}/${dx}`
      slopes.set(slope, (slopes.get(slope) || 0) + 1)
    }

    // 计算每个点的最多点数
    let localMax = duplicate
    for (let count of slopes.values()) {
      localMax = Math.max(localMax, count + duplicate)
    }

    maxCount = Math.max(maxCount, localMax)
  }

  return maxCount
}

// 求最大公约数
function gcd(a, b) {
  while (b !== 0) {
    let temp = b
    b = a % b
    a = temp
  }
  return a
}

33.存在重复元素 II-219

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [1,2,3,1], k = 3
输出：true

示例 2：

输入：nums = [1,0,1,1], k = 1
输出：true

示例 3：

输入：nums = [1,2,3,1,2,3], k = 2
输出：false

链接

思路：

1. 使用一个哈希表 map 来存储窗口内元素的索引。
2. 通过遍历数组，我们维护一个大小不超过 k 的滑动窗口。
3. 当遍历到 nums[i] 时：
   • 如果 nums[i] 在哈希表中存在，并且 i - map[nums[i]] <= k，则返回 true，表示找到了符合条件的两个元素。
   • 否则，更新哈希表，将 nums[i] 和其索引 i 放入哈希表。
   • 同时，如果窗口大小超过了 k，就将窗口的左边界元素移出窗口（即从哈希表中删除）。

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {boolean}
 */
var containsNearbyDuplicate = function (nums, k) {
  let map = new Map() // 哈希表，存储窗口中的元素和索引

  for (let i = 0; i < nums.length; i++) {
    if (map.has(nums[i]) && i - map.get(nums[i]) <= k) {
      return true // 找到符合条件的两个元素
    }

    // 更新哈希表中的元素索引
    map.set(nums[i], i)

    // 如果窗口大小超过k，移除左边界的元素
    if (map.size > k) {
      map.delete(nums[i - k])
    }
  }

  return false
}

存在重复元素-217

给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ，返回 true ；如果数组中每个元素互不相同，返回 false 。

示例 1：

**输入：**nums = [1,2,3,1]

**输出：**true

解释：

元素 1 在下标 0 和 3 出现。

示例 2：

**输入：**nums = [1,2,3,4]

**输出：**false

解释：

所有元素都不同。

示例 3：

**输入：**nums = [1,1,1,3,3,4,3,2,4,2]

**输出：**true

链接

思路

1. 使用哈希表：我们可以利用哈希表（或者 JavaScript 中的 Set）来解决这个问题。哈希表能够帮助我们快速判断某个元素是否已经出现过。
2. 遍历数组：我们遍历数组的每个元素，逐个检查该元素是否已经存在于哈希表中。如果存在，则说明有重复元素，直接返回 true。如果不存在，就将该元素加入到哈希表中。
3. 优化：哈希表查找、插入的平均时间复杂度是 O(1)，因此这个方法的时间复杂度为 O(n)，其中 n 是数组的长度。

/**
 * @param {number[]} nums
 * @return {boolean}
 */
var containsDuplicate = function (nums) {
  const seen = new Set() // 使用Set来存储已经出现过的元素

  for (let num of nums) {
    if (seen.has(num)) {
      return true // 如果当前数字已经在Set中出现过，说明有重复元素
    }
    seen.add(num) // 如果没有重复，就将当前数字加入Set
  }

  return false
}

存在重复元素 III-220

给你一个整数数组 nums 和两个整数 indexDiff 和 valueDiff 。

找出满足下述条件的下标对 (i, j)：

• i != j,
• abs(i - j) <= indexDiff
• abs(nums[i] - nums[j]) <= valueDiff

如果存在，返回 true *；*否则，返回 false 。

示例 1：

输入：nums = [1,2,3,1], indexDiff = 3, valueDiff = 0
输出：true
解释：可以找出 (i, j) = (0, 3) 。
满足下述 3 个条件：
i != j --> 0 != 3
abs(i - j) <= indexDiff --> abs(0 - 3) <= 3
abs(nums[i] - nums[j]) <= valueDiff --> abs(1 - 1) <= 0

示例 2：

输入：nums = [1,5,9,1,5,9], indexDiff = 2, valueDiff = 3
输出：false
解释：尝试所有可能的下标对 (i, j) ，均无法满足这 3 个条件，因此返回 false 。

反转链表-206

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL 进阶: 你可以迭代或递归地反转链表。你能否用两种方法解决这道题？ 链接：leetcode-cn.com/problems/reverse-linked-list

思路

记录一个 next 表示下一个节点， cur 表示当前节点，prev 表示上一个节点， 在循环中不断的把 cur.next 赋值为 prev，然后 cur 前进为刚刚保存的 next 节点，直到 cur 为 null。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function (head) {
  let prev = null
  let cur = head

  while (cur) {
    let next = cur.next
    cur.next = prev
    prev = cur
    cur = next
  }

  return prev
}

反转链表II-92

反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。

说明: 1 ≤ m ≤ n ≤ 链表长度。

示例:

输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL

链接

思路

这题相对于反转链表的第一题，就比较有难度了，所以说它是 medium 难度。

需要考虑的点很多：

1. 首先需要找出需要反转的链表的起点 node，终点 node。
2. 并且还需要记录下来需要反转的起点的前一个点 sliceStartPrev。
3. 需要反转的终点的后一个节点 sliceEndNext。
4. 在反转完成后要把起点的前一个节点的 sliceStartPrev 的 next 设为反转链表后的 head 头部。
5. 并且把反转后链表的 tail 尾部的 next 设置成 sliceEndNext。

当然，反转链表的部分还是可以沿用第一题的代码啦。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @param {number} m
 * @param {number} n
 * @return {ListNode}
 */

let reverseBetween = function (head, m, n) {
  let i = 1
  let sliceStartPrev = null
  let sliceStart = null
  let sliceEnd = null
  let cur = head

  // 记录切分起点的前一个节点，和切分终点的后一个节点
  while (i <= n) {
    if (i === m - 1) {
      sliceStartPrev = cur
    }
    if (i === m) {
      sliceStart = cur
    }
    if (i === n) {
      sliceEnd = cur
    }
    cur = cur.next
    i++
  }

  let sliceEndNext = sliceEnd.next
  // 切断切分终点的next 防止反转的时候反转过头
  sliceEnd.next = null

  const { head: slicedHead, tail: slicedTail } = reverse(sliceStart)
  if (sliceStartPrev) {
    // 如果需要反转的部分有前一个节点 那么只需要在中间动手脚 原样返回head节点即可
    sliceStartPrev.next = slicedHead
  } else {
    // 这里需要注意的是 如果没有sliceStartPrev 说明是从第一个节点就开始反转的
    // 那么我们需要手动调整head为反转后的head
    head = slicedHead
  }
  slicedTail.next = sliceEndNext

  return head
}

function reverse(head) {
  let prev = null
  let cur = head
  while (cur) {
    let next = cur.next
    cur.next = prev

    prev = cur
    cur = next
  }
  // 返回反转后的头尾节点
  return { head: prev, tail: head }
}

删除排序链表中的重复元素-83

给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。

示例 1：

输入：head = [1,1,2]
输出：[1,2]

示例 2：

输入：head = [1,1,2,3,3]
输出：[1,2,3]

链接

思路

1. 遍历链表：我们需要从头节点开始遍历链表。
2. 删除重复节点：对于每一个节点，如果当前节点的值与下一个节点的值相同，那么我们需要删除下一个节点（即跳过下一个节点）。
3. 更新指针：在遍历过程中，每次检查相邻节点的值是否相同，如果相同，则将当前节点的 next 指向下一个节点的 next，否则继续遍历下一个节点。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var deleteDuplicates = function (head) {
  let current = head

  while (current !== null && current.next !== null) {
    // 如果当前节点和下一个节点的值相同，跳过下一个节点
    if (current.val === current.next.val) {
      current.next = current.next.next
    } else {
      current = current.next // 否则继续移动到下一个节点
    }
  }

  return head
}

分隔链表-86

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当 保留 两个分区中每个节点的初始相对位置。

示例 1：

输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

示例 2：

输入：head = [2,1], x = 2
输出：[1,2]

链接

思路

1. 创建两个虚拟头节点：beforeHead 和 afterHead，分别表示小于 x 的链表和大于等于 x 的链表。

2. 遍历原链表

   • 如果当前节点值小于 x，将该节点追加到 before 链表。
   • 如果当前节点值大于或等于 x，将该节点追加到 after 链表。

3. 合并两个链表：将 before 链表的尾部连接到 afterHead 的头部，并设置 after 链表的尾节点为 null。

4. 返回 beforeHead.next 作为新链表的头。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} x
 * @return {ListNode}
 */
var partition = function (head, x) {
  // 创建两个虚拟头节点
  let beforeHead = new ListNode(0)
  let afterHead = new ListNode(0)

  let before = beforeHead // 小于x的链表
  let after = afterHead // 大于等于x的链表

  while (head !== null) {
    if (head.val < x) {
      before.next = head // 添加到before链表
      before = before.next
    } else {
      after.next = head // 添加到after链表
      after = after.next
    }
    head = head.next // 移动到下一个节点
  }

  // 断开after链表的最后一个节点
  after.next = null

  // 将两个链表链接
  before.next = afterHead.next

  return beforeHead.next
}

奇偶链表-328

给定单链表的头节点 head ，将所有索引为奇数的节点和索引为偶数的节点分别组合在一起，然后返回重新排序的列表。

第一个节点的索引被认为是 奇数 ， 第二个节点的索引为 偶数 ，以此类推。

请注意，偶数组和奇数组内部的相对顺序应该与输入时保持一致。

你必须在 O(1) 的额外空间复杂度和 O(n) 的时间复杂度下解决这个问题。

示例 1:

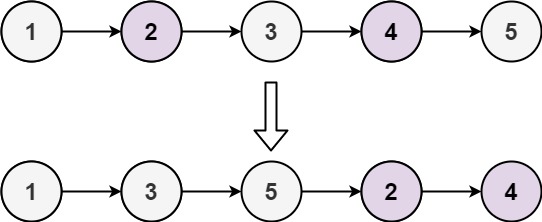
输入: head = [1,2,3,4,5]
输出: [1,3,5,2,4]

示例 2:

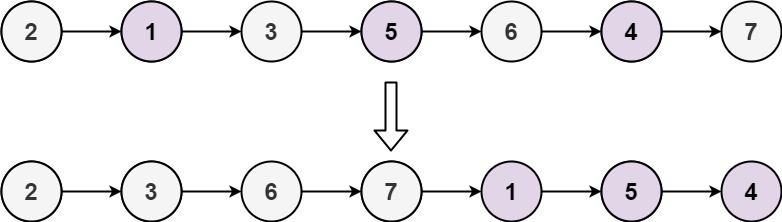
输入: head = [2,1,3,5,6,4,7]
输出: [2,3,6,7,1,5,4]

链接

思路

1. 初始化奇偶指针
   • 创建两个指针 odd 和 even，分别指向奇数节点和偶数节点。
   • 另有 evenHead 保存偶数链表的起始节点，便于最后合并链表。
2. 遍历链表
   • 通过移动指针将奇数节点链接到奇数链表，偶数节点链接到偶数链表。
3. 合并链表
   • 遍历完成后，将奇数链表的尾部与偶数链表的头部连接起来。
4. 返回奇数链表的头节点。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var oddEvenList = function (head) {
  if (!head || !head.next) return head // 如果链表为空或只有一个节点，直接返回

  let odd = head // 奇数链表的头节点
  let even = head.next // 偶数链表的头节点
  let evenHead = even // 读取偶数链表的起始节点

  while (even && even.next) {
    odd.next = even.next // 奇数指针调到下一个奇数节点
    odd = odd.next

    even.next = odd.next // 偶数指针跳到下一个偶数节点
    even = even.next
  }

  odd.next = evenHead // 合并奇数链表和偶数链表
  return head
}

两数相加-2

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

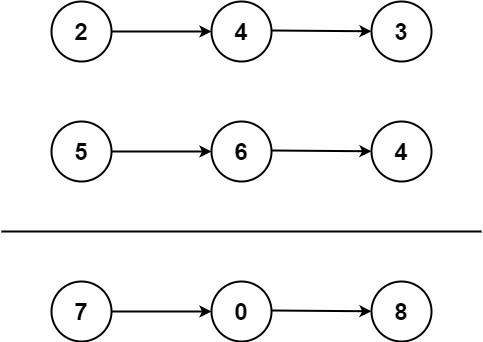
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

链接

解题思路

1. 逐位相加
   • 同时遍历两个链表，从最低位开始相加。
   • 记录每个位的进位。
2. 构建新链表
   • 将每次相加的结果作为新链表的一个节点。
3. 处理进位
   • 如果遍历结束后仍有进位，需要额外添加一个节点。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
var addTwoNumbers = function (l1, l2) {
  let dumyHead = new ListNode(0) // 哑节点，方便构建结果链表
  let current = dumyHead // 当前节点指针
  let carry = 0 // 进位

  while (l1 !== null || l2 !== null) {
    const val1 = l1 ? l1.val : 0 // 取出当前节点的值，若为空则为0
    const val2 = l2 ? l2.val : 0

    const sum = val1 + val2 + carry // 当前位的和
    carry = Math.floor(sum / 10) // 更新进位
    current.next = new ListNode(sum % 10) // 新节点存储当前位的值

    current = current.next // 移动指针
    if (l1) l1 = l1.next // 移动l1指针
    if (l2) l2 = l2.next // 移动l2指针
  }

  // 如果最后仍有进位，添加一个新节点
  if (carry > 0) {
    current.next = new ListNode(carry)
  }

  return dumyHead.next // 返回结果链表的头节点
}

移除链表元素-203

删除链表中等于给定值 val 的所有节点。

示例:
输入: 1->2->6->3->4->5->6, val = 6
输出: 1->2->3->4->5

leetcode-cn.com/problems/remove-linked-list-elements

思路

此题的主要思路是建立一个傀儡节点，这样在 while 循环中就只需要考虑对下一个节点的处理。

如果下一个节点值和目标值相同，那么就把 cur.next = cur.next.next 这样转移到下下个节点。

还有一个细节需要注意的是，如果下一个节点和目标值相同，此时循环中不需要用 cur = cur.next 把引用转移到下一个节点，因为此时自然而然的进入下一轮循环后，就会对 cur.next 也就是更改过后的待处理的 next 进行判断和处理。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} val
 * @return {ListNode}
 */
var removeElements = function (head, val) {
  let root = new ListNode()
  root.next = head
  let cur = root
  while (cur) {
    let next = cur.next
    if (!next) {
      break
    }
    let nextVal = next.val
    if (nextVal === val) {
      cur.next = cur.next.next
    } else {
      cur = cur.next
    }
  }
  return root.next
}

删除排序链表中的重复元素 II-82

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

示例 1：

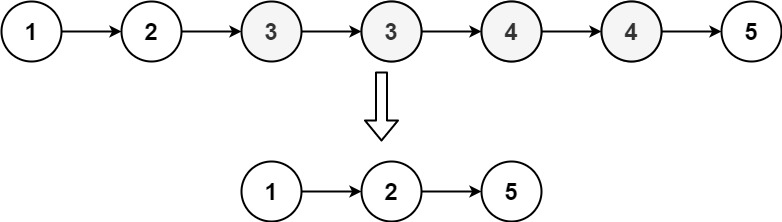
输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

示例 2：

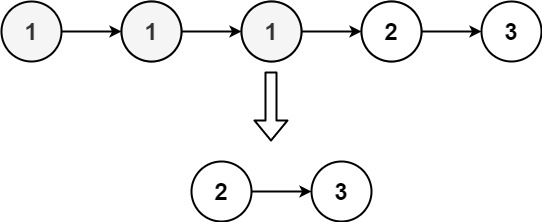
输入：head = [1,1,1,2,3]
输出：[2,3]

链接

解题思路

1. 哑节点：
   • 使用一个哑节点（dummy）指向链表头部，便于处理头部节点被删除的情况。
2. 双指针遍历：
   • 使用两个指针，一个是当前节点指针，一个是检查重复的指针。
   • 当检测到重复节点时，跳过所有重复的节点。
3. 删除逻辑：
   • 如果当前节点值与下一个节点值不同，移动当前指针。
   • 如果有重复，调整指针跳过所有重复节点。
4. 返回结果：
   • 返回哑节点的 next 即为新链表的头。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var deleteDuplicates = function (head) {
  if (!head || !head.next) {
    return head
  }

  let dummy = new ListNode(0, head) // 哑节点指向头部
  let prev = dummy // 前一个有效节点

  while (head && head.next) {
    if (head.val === head.next.val) {
      // 跳过所有重复值
      while (head.next && head.val === head.next.val) {
        head = head.next
      }
      // 删除重复节点
      prev.next = head.next
    } else {
      // 无重复，移动prev指针
      prev = prev.next
    }
    head = head.next // 移动head执行
  }

  return dummy.next
}

合并两个有序链表-21

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

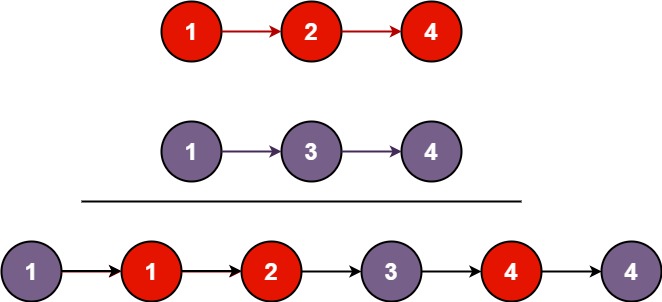
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

链接

解题思路

1. 双指针法：
   • 使用两个指针 l1 和 l2 分别指向两个链表的头部，逐一比较两个链表的节点值。
   • 每次选择较小的节点插入到新的链表中，并且移动相应链表的指针。
   • 如果某个链表已经遍历完，则直接将另一个链表剩下的部分连接到新链表的末尾。
2. 哑节点：
   • 为了方便处理链表的插入操作，我们可以使用一个哑节点（dummy node），它的 next 指向新链表的头部。
   • 最终返回哑节点的 next 即为合并后的链表。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} list1
 * @param {ListNode} list2
 * @return {ListNode}
 */
var mergeTwoLists = function (l1, l2) {
  let dummy = new ListNode(0) // 创建哑节点
  let current = dummy // 当前节点

  // 遍历两个链表，逐一比较节点
  while (l1 !== null && l2 !== null) {
    if (l1.val < l2.val) {
      current.next = l1 // 将l1的节点连接到新链表
      l1 = l1.next // 移动l1指针
    } else {
      current.next = l2 // 将l2的节点连接到新链表
      l2 = l2.next // 移动l2指针
    }
    current = current.next // 移动current指针
  }

  // 如果其中一个链表没有遍历完，直接将剩下的部分连接到新链表
  if (l1 !== null) {
    current.next = l1
  }
  if (l2 !== null) {
    current.next = l2
  }

  return dummy.next // 返回合并后的链表头部
}

两两交换链表中的节点-24

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例:

给定 1->2->3->4, 你应该返回 2->1->4->3.

链接：leetcode-cn.com/problems/swap-nodes-in-pairs

思路

这题本意比较简单，1 -> 2 -> 3 -> 4 的情况下可以定义一个递归的辅助函数 helper，这个辅助函数对于节点和它的下一个节点进行交换，比如 helper(1) 处理 1 -> 2，并且把交换变成 2 -> 1 的尾节点 1的next继续指向 helper(3)也就是交换后的 4 -> 3。

边界情况在于，如果顺利的作了两两交换，那么交换后我们的函数返回出去的是 交换后的头部节点，但是如果是奇数剩余项的情况下，没办法做交换，那就需要直接返回 原本的头部节点。这个在 helper函数和主函数中都有体现。

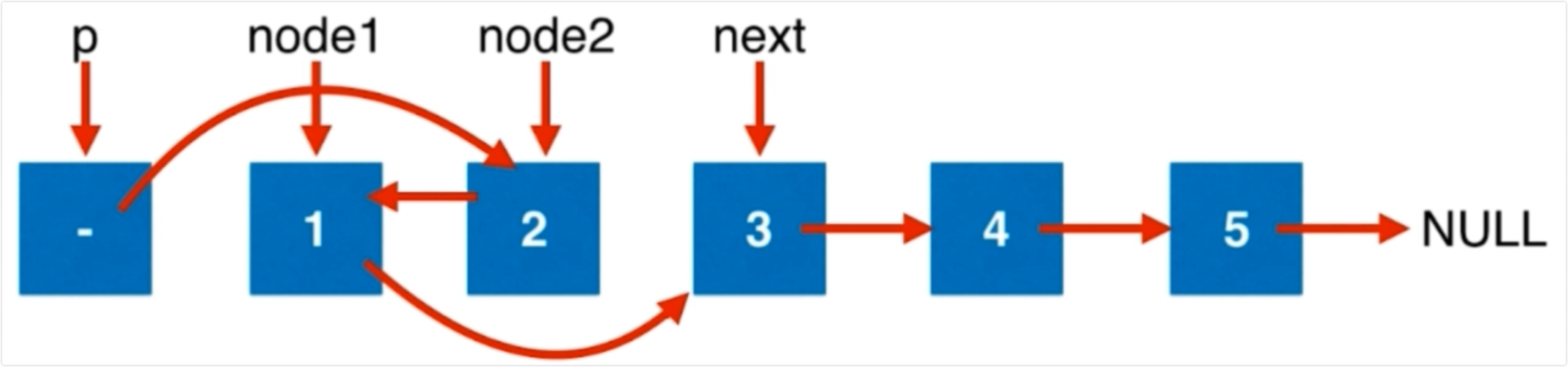
递归

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
let swapPairs = function (head) {
  if (!head) return null
  let helper = function (node) {
    let tempNext = node.next
    if (tempNext) {
      let tempNextNext = node.next.next
      node.next.next = node
      if (tempNextNext) {
        node.next = helper(tempNextNext)
      } else {
        node.next = null
      }
    }
    return tempNext || node
  }

  let res = helper(head)

  return res || head
}

迭代

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
let swapPairs = function (head) {
  let dummy = new ListNode(0) // 创建一个虚拟头节点
  dummy.next = head

  let current = dummy // 从虚拟头节点开始
  while (current.next && current.next.next) {
    let first = current.next // 第一个节点
    let second = current.next.next // 第二个节点

    // 交换两个节点
    first.next = second.next
    second.next = first
    current.next = second

    // 移动current到交换后的节点
    current = first
  }

  return dummy.next // 返回新的头节点
}

K 个一组翻转链表-25

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

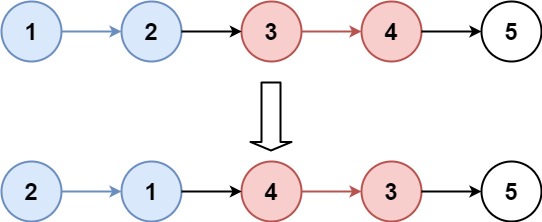
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

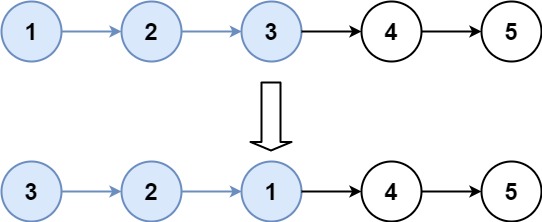
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

链接

思路

可以分为以下几个步骤：

1. 分组：找到每 k个一组的子链表。
2. 翻转：对每组链表进行翻转。
3. 连接：将翻转后的子链表重新拼接到主链表中。

需要注意边界条件，例如链表节点总数不足 k 的情况。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
var reverseKGroup = function (head, k) {
  // 边界情况：链表为空或只有一个节点，无需翻转
  if (!head || k === 1) {
    return head
  }

  let count = 0
  let current = head

  // 检查链表中是否有至少k个节点
  while (current && count < k) {
    current = current.next
    count++
  }

  // 如果有k个节点，翻转这k个节点
  if (count === k) {
    let reversedHead = reverse(head, k) // 翻转前k个节点
    // head时翻转后的尾节点，它的next需要执行后续处理的链表
    head.next = reverseKGroup(current, k) // 递归处理剩余链表
    return reversedHead
  }

  // 如果不足k个节点，直接返回原链表
  return head
}

// 辅助函数：繁殖链表前k个节点
function reverse(head, k) {
  let prev = null
  let current = head

  while (k > 0) {
    let next = current.next
    current.next = prev
    prev = current
    current = next
    k--
  }
  return prev // 返回翻转后的头节点
}

对链表进行插入排序-147

给定单个链表的头 head ，使用 插入排序 对链表进行排序，并返回 排序后链表的头 。

插入排序 算法的步骤:

1. 插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
2. 每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
3. 重复直到所有输入数据插入完为止。

下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时，从输入数据中删除一个元素(红色)，并就地插入已排序的列表中。

对链表进行插入排序。

示例 1：

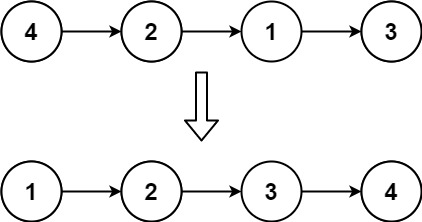
输入: head = [4,2,1,3]
输出: [1,2,3,4]

示例 2：

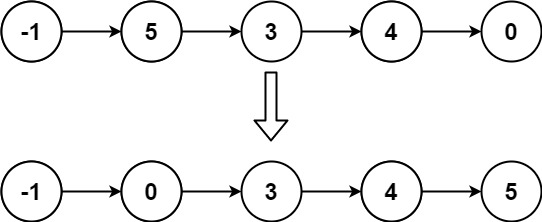
输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]

链接

思路

1. 虚拟头节点：
   • 使用虚拟头节点（dummy）方便操作，将所有插入操作连接到虚拟头节点后。
2. 逐一遍历：
   • 遍历链表的每个节点，将其插入到已排序部分的正确位置。
3. 寻找插入位置：
   • 使用双指针找到已排序部分中当前节点应插入的位置。
4. 插入操作：
   • 修改指针以完成插入。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var insertionSortList = function (head) {
  if (!head || !head.next) {
    return head // 链表为空或只有一个节点，无需排序
  }

  let dummy = new ListNode(0) // 创建虚拟头节点
  dummy.next = head

  let current = head // 当前处理节点
  while (current && current.next) {
    if (current.val <= current.next.val) {
      // 如果当前节点的值小于下一个节点，说明顺序正确，无需调整
      current = current.next
    } else {
      // 否则取出next节点病找到它的插入位置
      let toInsert = current.next // 带插入节点
      current.next = toInsert.next // 将toInsert节点从链表中移除

      // 找到插入位置：prev时已排序部分的指针
      let prev = dummy
      while (prev.next && prev.next.val < toInsert.val) {
        prev = prev.next
      }

      // 将toInsert插入到prev和prev.next之间
      toInsert.next = prev.next
      prev.next = toInsert
    }
  }

  return dummy.next // 返回排序厚的链表头节点
}

排序链表-148

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：

输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

输入：head = []
输出：[]

链接

思路

1. 拆分链表：
   • 使用快慢指针找到链表的中间节点，将链表拆分为两个子链表。
2. 递归排序：
   • 对拆分的两个子链表分别递归调用归并排序。
3. 合并两个有序链表：
   • 使用双指针合并两个已排序的链表。
4. 返回排序后的链表：
   • 递归的出口是链表为空或只有一个节点，直接返回。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var sortList = function (head) {
  if (!head || !head.next) {
    return head // 链表为空或只有一个节点，无需排序
  }

  // 使用快慢指针找到链表的中间节点
  let slow = head
  let fast = head
  let prev = null
  while (fast && fast.next) {
    prev = slow
    slow = slow.next
    fast = fast.next.next
  }
  prev.next = null // 将链表断开，分成两部分

  // 递归排序左右两部分
  let left = sortList(head)
  let right = sortList(slow)

  // 合并两个有序链表
  return merge(left, right)
}

function merge(l1, l2) {
  let dummy = new ListNode(0) // 虚拟头节点
  let current = dummy

  while (l1 && l2) {
    if (l1.val < l2.val) {
      current.next = l1
      l1 = l1.next
    } else {
      current.next = l2
      l2 = l2.next
    }
    current = current.next
  }

  // 链接剩余节点
  current.next = l1 || l2

  return dummy.next
}

删除链表中的节点-237

有一个单链表的 head，我们想删除它其中的一个节点 node。

给你一个需要删除的节点 node 。你将 无法访问 第一个节点 head。

链表的所有值都是 唯一的，并且保证给定的节点 node 不是链表中的最后一个节点。

删除给定的节点。注意，删除节点并不是指从内存中删除它。这里的意思是：

• 给定节点的值不应该存在于链表中。
• 链表中的节点数应该减少 1。
• node 前面的所有值顺序相同。
• node 后面的所有值顺序相同。

自定义测试：

• 对于输入，你应该提供整个链表 head 和要给出的节点 node。node 不应该是链表的最后一个节点，而应该是链表中的一个实际节点。
• 我们将构建链表，并将节点传递给你的函数。
• 输出将是调用你函数后的整个链表。

示例 1：

输入：head = [4,5,1,9], node = 5
输出：[4,1,9]
解释：指定链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9

示例 2：

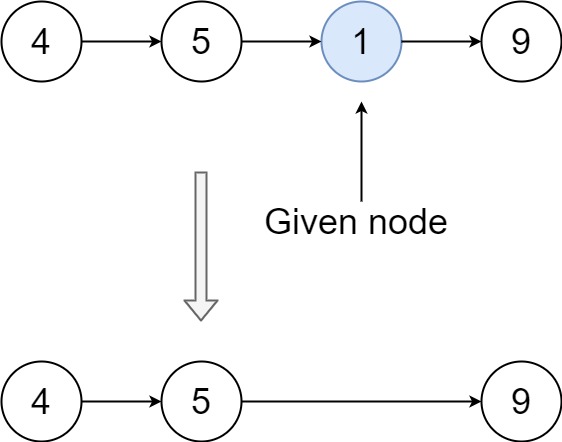
输入：head = [4,5,1,9], node = 1
输出：[4,5,9]
解释：指定链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9

链接

思路

由于我们无法访问前一个节点，只能操作当前节点及其后续部分，因此可以采用以下方法：

1. 将要删除节点的值替换为其下一个节点的值。
2. 跳过下一个节点，即将当前节点的 next 指针指向其下下一个节点。

此方法的核心在于：

• 将 node 的值更改为 node.next 的值，变相实现了当前节点的“删除”。
• 更新 node.next 指针以跳过下一个节点。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} node
 * @return {void} Do not return anything, modify node in-place instead.
 */
var deleteNode = function (node) {
  if (node === null || node.next === null) {
    return
  }

  // 将当前节点的值替换为下一个节点的值
  node.val = node.next.val
  // 跳过下一个节点
  node.next = node.next.next
}

删除链表的倒数第 N 个结点-19

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

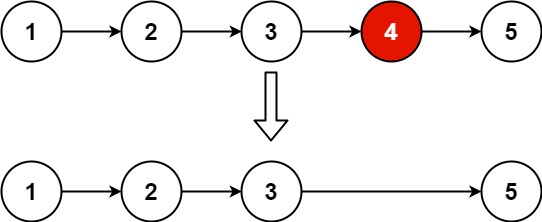
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

链表

思路

1. 双指针法：
   • 初始化两个指针 fast 和 slow，都指向链表的头节点。
   • 让 fast 指针先向前移动 n步，这样 fast 和 slow 之间相隔 n 个节点。
   • 然后同时移动 fast 和 slow，直到 fast 到达链表末尾，此时 slow 正好位于要删除节点的前一个节点。
   • 修改 slow.next，跳过需要删除的节点。
2. 边界处理：
   • 如果删除的是链表的第一个节点（倒数第 nnn 个节点也是头节点），需要特殊处理。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} n
 * @return {ListNode}
 */
var removeNthFromEnd = function (head, n) {
  // 创建哑节点，方便处理头节点的删除
  let dummy = new ListNode(0, head)
  let fast = dummy
  let slow = dummy

  // 让fast指针先前进n+1步
  for (let i = 0; i <= n; i++) {
    fast = fast.next
  }

  // 同时移动fast和slow，知道fast到达末尾
  while (fast !== null) {
    fast = fast.next
    slow = slow.next
  }

  // 删除倒数第n个节点
  slow.next = slow.next.next

  // 返回头节点
  return dummy.next
}

旋转链表-61

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]

示例 2：

输入：head = [0,1,2], k = 4
输出：[2,0,1]

链接

思路

1. 确定链表的长度：
   • 首先遍历一次链表，得到链表的长度 n。
2. 处理 k 大于 n 的情况：
   • 旋转 k 次实际上相当于旋转 k mod  n 次，因此 k 可以取模链表长度。
3. 旋转链表：
   • 将链表断开，并将尾部部分连接到链表的头部。具体来说，首先找到倒数第 k 个节点，并断开链表，将该节点的下一个节点设置为新的头节点，之前的头节点连接到原来链表的尾节点。
4. 边界情况：
   • 当链表为空或 k=0或 k是链表长度的整数倍时，旋转后的链表不变。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val);
 *     this.next = (next===undefined ? null : next);
 * }
 */

/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
var rotateRight = function (head, k) {
  if (!head || !head.next || k === 0) {
    return head
  }

  // 计算链表长度
  let length = 1
  let current = head
  while (current.next) {
    length++
    current = current.next
  }

  // 计算有效的旋转次数
  k = k % length
  if (k === 0) {
    return head
  }

  // 将链表连接成环
  current.next = head

  // 找到倒数第 k 个节点
  let stepsToNewHead = length - k
  let newTail = head
  for (let i = 1; i < stepsToNewHead; i++) {
    newTail = newTail.next
  }

  // 新的头节点是 newTail.next
  let newHead = newTail.next
  // 断开链表环
  newTail.next = null

  return newHead
}

重排链表-143

给定一个单链表 L 的头节点 head ，单链表 L 表示为：

L0 → L1 → … → Ln - 1 → Ln

请将其重新排列后变为：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1：

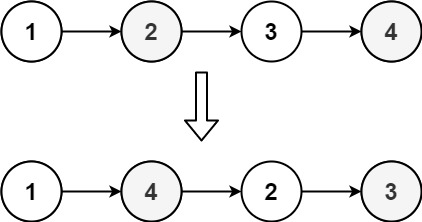
输入：head = [1,2,3,4]
输出：[1,4,2,3]

示例 2：

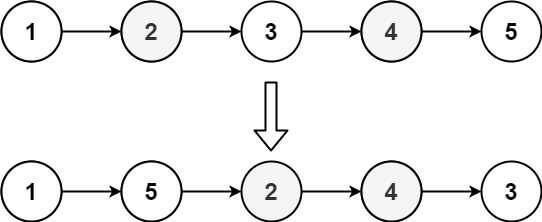
输入：head = [1,2,3,4,5]
输出：[1,5,2,4,3]

链接

思路

为了完成这个操作，首先需要将链表分为两部分，一部分是前半部分，另一部分是后半部分。然后按照要求将这两部分交替合并。

具体步骤如下：

1. 找到链表的中点：
   • 使用快慢指针的方式，快指针每次走两步，慢指针每次走一步，最终慢指针会指向链表的中点。
2. 拆分链表：
   • 将链表从中点分为两部分，第一部分是前半部分，第二部分是后半部分。
3. 反转第二部分链表：
   • 对第二部分链表进行反转，这样可以方便我们将两个链表交替合并。
4. 交替合并两个链表：
   • 将第一部分的节点与第二部分（反转后的）节点交替合并。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val);
 *     this.next = (next===undefined ? null : next);
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reorderList = function (head) {
  if (!head || !head.next) {
    return head // 如果链表为空或只有一个节点，直接返回
  }

  // 步骤 1: 使用快慢指针找到链表的中点
  let slow = head
  let fast = head

  // 快指针每次走两步，慢指针每次走一步，最终慢指针会到达链表中点
  while (fast && fast.next) {
    slow = slow.next
    fast = fast.next.next
  }

  // 步骤 2: 分割链表
  let second = slow.next
  slow.next = null // 断开链表，前半部分的尾部指向 null

  // 步骤 3: 反转第二部分链表
  second = reverseList(second)

  // 步骤 4: 交替合并两个链表
  let first = head
  while (second) {
    let tmp1 = first.next
    let tmp2 = second.next

    first.next = second // 将第一部分的节点连接到第二部分的节点
    second.next = tmp1 // 将第二部分的节点连接到第一部分的下一个节点

    first = tmp1 // 第一部分的指针移动到下一个节点
    second = tmp2 // 第二部分的指针移动到下一个节点
  }

  return head
}

/**
 * 反转链表
 * @param {ListNode} head
 * @return {ListNode}
 */
function reverseList(head) {
  let prev = null
  let curr = head

  while (curr) {
    let nextTemp = curr.next
    curr.next = prev
    prev = curr
    curr = nextTemp
  }

  return prev
}

回文链表234

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：head = [1,2,2,1]
输出：true

示例 2：

输入：head = [1,2]
输出：false

链接

思路

1. 使用快慢指针找到链表的中点：
   • 使用快慢指针方法，快指针每次走两步，慢指针每次走一步。最终，慢指针会指向链表的中点。
2. 反转链表的后半部分：
   • 在找到链表的中点后，将后半部分链表反转。这是因为回文链表的性质是前半部分与后半部分的逆序相等，所以反转后半部分可以帮助我们比较两部分是否相等。
3. 比较两部分链表：
   • 从头节点和反转后的后半部分同时遍历链表，逐一比较每个节点的值。如果所有节点都相等，那么链表是回文的；否则不是。
4. 恢复链表（可选）：
   • 如果需要保留原链表结构，可以在完成比较后，将后半部分链表反转回原样。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {boolean}
 */
var isPalindrome = function (head) {
  if (!head || !head.next) {
    return true // 空链表或只有一个节点是回文串
  }

  // 1.使用快慢指针找到链表的中点
  let slow = head
  let fast = head

  // 快指针每次走两步，慢指针每次走一步
  while (fast && fast.next) {
    slow = slow.next
    fast = fast.next.next
  }

  // 2.翻转后半部分链表
  let secondHalf = reverseList(slow)

  // 3.比较前半部分和翻转后的后半部分
  let firstHalf = head
  while (secondHalf) {
    if (firstHalf.val !== secondHalf.val) {
      return false // 如果不相等，返回false
    }
    firstHalf = firstHalf.next
    secondHalf = secondHalf.next
  }

  return true // 如果所有节点都相等，则是回文链表
}

// 反转链表
function reverseList(head) {
  let prev = null
  let curr = head

  while (curr) {
    let nextTemp = curr.next
    curr.next = prev
    prev = curr
    curr = nextTemp
  }
  return prev // 返回反转后的链表头
}

有效的括号-20

20.有效的括号 给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 注意空字符串可被认为是有效字符串。

示例 1:

输入: "()"
输出: true

示例 2:

输入: "()[]{}"
输出: true

示例 3:

输入: "(]"
输出: false

示例 4:

输入: "([)]"
输出: false

示例 5:

输入: "{[]}"
输出: true

leetcode-cn.com/problems/valid-parentheses

思路

提前记录好左括号类型 (, {, [和右括号类型), }, ]的映射表，当遍历中遇到左括号的时候，就放入栈 stack 中（其实就是数组），当遇到右括号时，就把 stack 顶的元素 pop 出来，看一下是否是这个右括号所匹配的左括号（比如 ( 和 ) 是一对匹配的括号）。

当遍历结束后，栈中不应该剩下任何元素，返回成功，否则就是失败。

/**
 * @param {string} s
 * @return {boolean}
 */
let isValid = function (s) {
  let sl = s.length
  if (sl % 2 !== 0) return false
  let leftToRight = {
    '{': '}',
    '[': ']',
    '(': ')'
  }
  // 建立一个反向的 value -> key 映射表
  let rightToLeft = createReversedMap(leftToRight)
  // 用来匹配左右括号的栈
  let stack = []

  for (let i = 0; i < s.length; i++) {
    let bracket = s[i]
    // 左括号 放进栈中
    if (leftToRight[bracket]) {
      stack.push(bracket)
    } else {
      let needLeftBracket = rightToLeft[bracket]
      // 左右括号都不是 直接失败
      if (!needLeftBracket) {
        return false
      }

      // 栈中取出最后一个括号 如果不是需要的那个左括号 就失败
      let lastBracket = stack.pop()
      if (needLeftBracket !== lastBracket) {
        return false
      }
    }
  }

  if (stack.length) {
    return false
  }
  return true
}

function createReversedMap(map) {
  return Object.keys(map).reduce((prev, key) => {
    const value = map[key]
    prev[value] = key
    return prev
  }, {})
}

/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function (s) {
  // 使用栈保存左括号
  const stack = []
  // 定义括号的映射关系
  const map = {
    ')': '(',
    '}': '{',
    ']': '['
  }

  // 遍历字符串
  for (const char of s) {
    if (char in map) {
      // 当前字符是右括号
      const top = stack.length > 0 ? stack.pop() : '#' // 栈顶字符
      if (top !== map[char]) {
        return false // 不匹配则无效
      }
    } else {
      // 当前字符是左括号，入栈
      stack.push(char)
    }
  }

  // 检查栈是否为空
  return stack.length === 0
}

逆波兰表达式求值-150

150.逆波兰表达式求值 根据逆波兰表示法，求表达式的值。

有效的运算符包括 +, -, *, / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。 示例 1：

输入: ["2", "1", "+", "3", "*"]
输出: 9
解释: ((2 + 1) * 3) = 9

示例 2：

输入: ["4", "13", "5", "/", "+"]
输出: 6
解释: (4 + (13 / 5)) = 6

leetcode-cn.com/problems/evaluate-reverse-polish-notation

思路

提前声明好运算符对应的运算函数，当遇到数字时就放进栈中，遇到运算符，就 pop 出栈中的两个数据，对它们使用运算函数，把结果继续放入栈中即可。

运算到最后，栈中剩下的唯一元素就是最后的结果。

/**
 * @param {string[]} tokens
 * @return {number}
 */
var evalRPN = function (tokens) {
  const stack = []

  for (const token of tokens) {
    if (['+', '-', '*', '/'].includes(token)) {
      // 遇到运算符，取出栈顶两个元素
      const b = stack.pop()
      const a = stack.pop()
      let result
      switch (token) {
        case '+':
          result = a + b
          break
        case '-':
          result = a - b
          break
        case '*':
          result = a * b
          break
        case '/':
          result = Math.trunc(a / b) // 使用 Math.trunc 保留整数部分
          break
      }
      stack.push(result) // 将结果入栈
    } else {
      // 遇到数字，转换为整数后入栈
      stack.push(parseInt(token, 10))
    }
  }

  return stack[0] // 栈中最后剩下的就是结果
}

简化路径-71

71.简化路径

以 Unix 风格给出一个文件的绝对路径，你需要简化它。或者换句话说，将其转换为规范路径。

在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （..） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。更多信息请参阅：Linux / Unix 中的绝对路径 vs 相对路径

请注意，返回的规范路径必须始终以斜杠 / 开头，并且两个目录名之间必须只有一个斜杠 /。最后一个目录名（如果存在）不能以 / 结尾。此外，规范路径必须是表示绝对路径的最短字符串。

示例 1：

输入："/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。
示例 2：

输入："/../"
输出："/"
解释：从根目录向上一级是不可行的，因为根是你可以到达的最高级。
示例 3：

输入："/home//foo/"
输出："/home/foo"
解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。
示例 4：

输入："/a/./b/../../c/"
输出："/c"
示例 5：

输入："/a/../../b/../c//.//"
输出："/c"
示例 6：

输入："/a//b////c/d//././/.."
输出："/a/b/c"

leetcode-cn.com/problems/simplify-path

思路

这题看似很复杂，但是其实用栈来做还是蛮简单的，先用 / 来分割路径字符串，然后不停的把分割后的有效值 push 到栈中即可，

注意的点：

1. 有效值的定义是：非 '..'、'.'、'' 这些特殊值以外的值。
2. 遇到 .. 字符，说明要回退一级目录，把栈中弹出一个值即可。
3. 最后返回的字符串值要特殊处理下，如果最后是空字符的话，直接返回 '/'，否则把末尾的 '/' 给去掉后返回

/**
 * @param {string} path
 * @return {string}
 */
var simplifyPath = function (path) {
  let tokens = path.split('/')
  let stack = []

  for (let index = 0; index < tokens.length; index++) {
    let token = tokens[index]
    if (token === '..') {
      if (stack.length > 0) {
        stack.pop()
      }
    } else if (!(token === '') && !(token === '.')) {
      stack.push(token)
    }
  }

  let res = '/'
  for (let token of stack) {
    res += `${token}/`
  }
  if (res !== '/') {
    res = res.substr(0, res.length - 1)
  }
  return res
}

扁平化嵌套列表迭代器-341

给你一个嵌套的整数列表 nestedList 。每个元素要么是一个整数，要么是一个列表；该列表的元素也可能是整数或者是其他列表。请你实现一个迭代器将其扁平化，使之能够遍历这个列表中的所有整数。

实现扁平迭代器类 NestedIterator ：

• NestedIterator(List<NestedInteger> nestedList) 用嵌套列表 nestedList 初始化迭代器。
• int next() 返回嵌套列表的下一个整数。
• boolean hasNext() 如果仍然存在待迭代的整数，返回 true ；否则，返回 false 。

你的代码将会用下述伪代码检测：

initialize iterator with nestedList
res = []
while iterator.hasNext()
    append iterator.next() to the end of res
return res

如果 res 与预期的扁平化列表匹配，那么你的代码将会被判为正确。

示例 1：

输入：nestedList = [[1,1],2,[1,1]]
输出：[1,1,2,1,1]
解释：通过重复调用 next 直到 hasNext 返回 false，next 返回的元素的顺序应该是: [1,1,2,1,1]。

示例 2：

输入：nestedList = [1,[4,[6]]]
输出：[1,4,6]
解释：通过重复调用 next 直到 hasNext 返回 false，next 返回的元素的顺序应该是: [1,4,6]。

链接

思路

1. 构造函数 NestedIterator(nestedList)：初始化时，我们会把整个 nestedList 压入栈中，并按正确的顺序进行处理（从最后一个元素开始，确保栈顶元素可以依次被处理）。
2. hasNext()：检查当前栈顶元素。如果是整数，直接返回 true；如果是列表，展开它并将列表中的元素压入栈中，直到栈顶元素是整数或栈为空。
3. next()：返回栈顶的整数，并移除栈顶元素。

/**
 * // This is the interface that allows for creating nested lists.
 * // You should not implement it, or speculate about its implementation
 * function NestedInteger() {
 *
 *     Return true if this NestedInteger holds a single integer, rather than a nested list.
 *     @return {boolean}
 *     this.isInteger = function() {
 *         ...
 *     };
 *
 *     Return the single integer that this NestedInteger holds, if it holds a single integer
 *     Return null if this NestedInteger holds a nested list
 *     @return {integer}
 *     this.getInteger = function() {
 *         ...
 *     };
 *
 *     Return the nested list that this NestedInteger holds, if it holds a nested list
 *     Return null if this NestedInteger holds a single integer
 *     @return {NestedInteger[]}
 *     this.getList = function() {
 *         ...
 *     };
 * };
 */
/**
 * @constructor
 * @param {NestedInteger[]} nestedList
 */
var NestedIterator = function (nestedList) {
  // 用栈来存储待遍历的元素，反向压入栈，确保我们能按顺序遍历
  this.stack = []
  for (let i = nestedList.length - 1; i >= 0; i--) {
    this.stack.push(nestedList[i])
  }
}

/**
 * @this NestedIterator
 * @returns {boolean}
 */
NestedIterator.prototype.hasNext = function () {
  // 确保栈顶是整数
  while (this.stack.length > 0) {
    let top = this.stack[this.stack.length - 1]
    if (top.isInteger()) {
      return true
    } else {
      // 如果栈顶时列表，则展开这个列表
      this.stack.pop() // 弹出这个列表
      let list = top.getList()
      for (let i = list.length - 1; i >= 0; i--) {
        this.stack.push(list[i]) // 将列表中的元素反向压入栈
      }
    }
  }
  return false
}

/**
 * @this NestedIterator
 * @returns {integer}
 */
NestedIterator.prototype.next = function () {
  // hasNext() 确保栈顶是整数，直接返回栈顶的整数病弹出
  return this.stack.pop().getInteger()
}

/**
 * Your NestedIterator will be called like this:
 * var i = new NestedIterator(nestedList), a = [];
 * while (i.hasNext()) a.push(i.next());
 */

二叉树的层序遍历-102

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：

二叉树：[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

链接：leetcode-cn.com/problems/binary-tree-level-order-traversal 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

经典模板题，DFS 和 BFS 都可以。

DFS

遍历的时候记录一下 level，每次递归都把 level+1，即可获得正确的层级，push 到对应的数组中即可：

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function (root) {
  let res = []
  let dfs = (node, level = 0) => {
    if (!node) return
    if (!res[level]) {
      res[level] = []
    }
    res[level].push(node.val)
    dfs(node.left, level + 1)
    dfs(node.right, level + 1)
  }
  dfs(root)
  return res
}

BFS

利用队列，while 中对于每轮的节点开一个 for 循环加入到数组的一层中即可。

/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
let levelOrder = function (root) {
  if (!root) return []
  let ret = []
  let queue = [root]

  while (queue.length) {
    let len = queue.length
    let level = []
    ret.push(level)
    for (let i = 0; i < len; i++) {
      let node = queue.shift()
      level.push(node.val)

      if (node.left) {
        queue.push(node.left)
      }
      if (node.right) {
        queue.push(node.right)
      }
    }
  }

  return ret
}

二叉树的层序遍历 II-107

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

链接

思路

1. 层序遍历：传统的层序遍历是从根节点到叶子节点的顺序，逐层从左到右。要实现自底向上的层序遍历，我们可以先进行常规的层序遍历，然后反转结果。
2. 使用队列进行层序遍历：为了实现层序遍历，我们可以使用广度优先搜索（BFS），通过队列来逐层处理树节点。
3. 从叶子节点到根节点的顺序：通过 BFS 遍历每一层节点，并将每一层的节点值保存到一个临时结果中。遍历结束后，将结果反转，得到自底向上的顺序。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrderBottom = function (root) {
  if (!root) return [] // 如果树为空，直接返回空数组

  let result = []
  let queue = [root] // 使用队列进行层序遍历

  while (queue.length > 0) {
    let levelSize = queue.length // 当前层的节点数
    let levelNodes = []

    // 遍历当前层的所有节点
    for (let i = 0; i < levelSize; i++) {
      let node = queue.shift() // 弹出队列中的节点
      levelNodes.push(node.val) // 将当前节点的值加入当前层的结果

      // 将左右子节点加入队列
      if (node.left) queue.push(node.left)
      if (node.right) queue.push(node.right)
    }

    result.push(levelNodes) // 将当前层的结果添加到最终结果中
  }

  // 反转最终结果，得到自底向上的层序遍历
  return result.reverse()
}

二叉树的右视图-199

199.二叉树的右视图

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例:

输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:

   1            <---
 /   \
2     3         <---
 \     \
  5     4       <---

leetcode-cn.com/problems/binary-tree-right-side-view

思路

基本上还是二叉树 BFS 的标准模板套上去就好了，只是取值的时候每一层取最右边的值，也就是从左到右遍历的时候记录到的最后一个值即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var rightSideView = function (root) {
  if (!root) return []
  let queue = [root]
  let res = []
  while (queue.length) {
    let len = queue.length
    let last
    for (let i = 0; i < len; i++) {
      let node = queue.shift()
      if (node.left) {
        queue.push(node.left)
      }
      if (node.right) {
        queue.push(node.right)
      }
      if (node.val !== undefined) {
        last = node.val
      }
    }
    res.push(last)
  }
  return res
}

完全平方数-279

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12 输出: 3 解释: 12 = 4 + 4 + 4. 示例 2:

输入: n = 13 输出: 2 解释: 13 = 4 + 9.

来源：力扣（LeetCode）链接：leetcode-cn.com/problems/perfect-squares 著 作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这个问题完全可以转化成 DP 问题。

对于求 f(12)来说，可以转化为求 f(12 - 任意一个平方数) + 1。

这个 + 1 是由于我们选出了一个平方数，所以也会算作凑目标值的次数。

那么假设这个平方数是 n，就在求解 12 的这一次循环里，不断的从 1 开始递增这个平方 数 1、2、4、8 .... 直到 12 - n < 0 中断，在这个过程中去找到能凑成 12 的最小的次 数。由于动态规划是自底向上的，f(12 - n) 是已经求好的值，那么结果就很容易得出了。

/**
 * @param {number} n
 * @return {number}
 */
var numSquares = function (n) {
  let dp = []

  // 求0就假设为0次
  dp[0] = 0

  for (let i = 1; i <= n; i++) {
    let j = 1
    // 初始化为Ininity 这样后面任意一个小值都可以覆盖他
    let min = Infinity
    while (true) {
      // 用i减去不断递增的平方数 j*j
      let prev = i - j * j
      if (prev < 0) {
        break
      }

      // 假设i=10，j=1实际上就是在求dp[10-1]+1
      // 也就是凑成9的最小次数，再加上1（也就是1这个平方数的次数）
      min = Math.min(min, dp[prev] + 1)
      j++
    }
    dp[i] = min === Infinity ? 0 : min
  }

  return dp[n]
}

前 K 个高频元素-347

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

如果不需要特别高效的实现，可以直接使用 JavaScript 内置的 .sort() 方法来模拟堆操作。你可以通过控制 k 的大小，避免进行完整的排序。

var topKFrequent = function (nums, k) {
  let res = [],
    map = new Map()

  // 统计频率
  nums.forEach((n) => map.set(n, map.get(n) + 1 || 1))

  // 按照频率排序
  let sortedArray = [...map.entries()].sort((a, b) => b[1] - a[1])

  // 返回前 k 个频率最高的元素
  for (let i = 0; i < k; i++) {
    res.push(sortedArray[i][0])
  }

  return res
}

二叉树的最大深度-104

104.二叉树的最大深度 给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。

leetcode-cn.com/problems/maximum-depth-of-binary-tree

思路

DFS

简单的 DFS 思路就是递归的遍历整个子树，每递归一个子节点就把传入的 depth 参数 +1，并且去对比全局保存的最大值变量 max 并且更新。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function (root) {
  let max = 0
  let helper = (node, depth) => {
    if (!node) return
    max = Math.max(max, depth)
    if (node.left) {
      helper(node.left, depth + 1)
    }
    if (node.right) {
      helper(node.right, depth + 1)
    }
  }
  helper(root, 1)
  return max
}

BFS

BFS 的思路还是套标准模板，每次循环是一层的分界点，在每轮循环中不停的把下一层的子节点加入到队列中，下次循环则继续处理这些子节点，并且每轮循环都把 max + 1，这样最后的 max 就是最大的深度了。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
let maxDepth = function (root) {
  if (!root) return 0
  let max = 0
  let queue = [root]

  while (queue.length) {
    max += 1
    let len = queue.length
    while (len--) {
      let node = queue.shift()
      if (node.left) {
        queue.push(node.left)
      }
      if (node.right) {
        queue.push(node.right)
      }
    }
  }

  return max
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function (root) {
  if (!root) return 0
  return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
}

二叉树的最小深度-111

111.二叉树的最小深度 给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回它的最小深度  2.

思路

DFS

记录一个最小值 min，每当 DFS 到节点既没有左节点也没有右节点，就更新这个 min 值，整个树遍历完成后返回这个 min 即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function (root) {
  let min = Infinity
  let helper = (node, depth) => {
    if (!node) return
    if (!node.left && !node.right) {
      min = Math.min(min, depth)
      return
    }
    if (node.left) {
      helper(node.left, depth + 1)
    }
    if (node.right) {
      helper(node.right, depth + 1)
    }
  }
  helper(root, 1)
  return min === Infinity ? 0 : min
}

BFS

这题用 BFS 可能可以更快的找到答案，因为 DFS 必须要遍历完整棵树才可以确定结果，但是 BFS 的话由于层级是从低到高慢慢增加的遍历，所以发现某一层的某个节点既没有左节点又没有右节点的话，就可以直接返回当前的层级作为答案了。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function (root) {
  if (!root) return 0

  let depth = 0
  let queue = [root]

  while (queue.length) {
    depth++
    let len = queue.length
    while (len--) {
      let node = queue.shift()

      let left = node.left
      let right = node.right
      if (!left && !right) {
        return depth
      }

      if (left) {
        queue.push(left)
      }
      if (right) {
        queue.push(right)
      }
    }
  }
}

翻转二叉树-226

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

链接

思路：

• 对每个节点，将其左子节点和右子节点交换。
• 然后递归调用其左右子节点，直到树的所有节点都完成交换。

时间复杂度：

• 每个节点访问一次，时间复杂度是 O(n)，其中 n 是节点数量。

空间复杂度：

• 最坏情况下递归深度为树的高度，空间复杂度是 O(h)，其中 h 是树的高度。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function (root) {
  if (!root) {
    return null
  }

  // 交换当前节点的左右子节点
  ;[root.left, root.right] = [root.right, root.left]

  // 递归翻转左右子树
  invertTree(root.left)
  invertTree(root.right)

  return root
}

相同的树-100

给定两个二叉树，编写一个函数来检验它们是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1:

输入:       1         1
          / \       / \
         2   3     2   3

        [1,2,3],   [1,2,3]

输出: true
示例 2:

输入:      1          1
          /           \
         2             2

        [1,2],     [1,null,2]

输出: false
示例 3:

输入:       1         1
          / \       / \
         2   1     1   2

        [1,2,1],   [1,1,2]

输出: false

链接：leetcode-cn.com/problems/same-tree

思路

DFS

深度优先遍历就是直接递归比较，把 left 和 right 节点也视为一棵树。继续调用 isSameTree 方法。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function (p, q) {
  if (!p && !q) return true
  if ((p && !q) || (!p && q)) return false

  if (isSameTree(p.left, q.left) && isSameTree(p.right, q.right)) {
    return p.val === q.val
  } else {
    return false
  }
}

BFS

BFS 也是标准的思路，就是把节点放进一个队列里，然后在处理节点的时候遇到有 left 或 right 子节点，就继续放进队列里，下一轮循环继续处理。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function (p, q) {
  let queue1 = [p]
  let queue2 = [q]

  while (queue1.length) {
    let node1 = queue1.shift()
    let node2 = queue2.shift()

    if (!node1 || !node2) {
      if (node1 !== node2) {
        return false
      }
      continue
    }

    if (node1.val !== node2.val) {
      return false
    }

    queue1.push(node1.left)
    queue1.push(node1.right)
    queue2.push(node2.left)
    queue2.push(node2.right)
  }

  return true
}

对称二叉树-101

101.对称二叉树 给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3


但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

思路

当一个二叉树对称时，说明它的左子树的左节点和右子树的右节点对称，并且左子树的右节点和右子树的左节点也对称。

根节点 root 可以同时当做最初的左节点和右节点，可以简化这个问题的判断。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function (root) {
  if (!root) {
    return true
  }
  let helper = (left, right) => {
    if (!left && !right) {
      return true
    }
    if (!left || !right) {
      return false
    }
    if (left.val === right.val) {
      return helper(left.left, right.right) && helper(left.right, right.left)
    } else {
      return false
    }
  }
  return helper(root, root)
}

完全二叉树的节点个数-222

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

[链接/]https://leetcode.cn/problems/count-complete-tree-nodes/description()

思路：

1. 对每个节点，递归计算其左右子树的节点总数。
2. 节点总数为：1 + 左子树节点数 + 右子树节点数。

时间复杂度：

• 最坏情况下 O(n)（树不平衡时相当于遍历每个节点一次）。

空间复杂度：

• 递归深度为树的高度，最坏情况下 O(h)，其中 h 是树的高度。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var countNodes = function (root) {
  if (!root) return 0
  // 递归计算左右子树的节点数
  return 1 + countNodes(root.left) + countNodes(root.right)
}

平衡二叉树-110

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7
返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4
返回 false 。

链接：leetcode-cn.com/problems/balanced-binary-tree

思路

首先定义一个辅助函数 getHeight 用于获取二叉树某个节点的高度，只需要递归即可：

function getHeight(node) {
  if (!node) return 0
  return Math.max(getHeight(node.left), getHeight(node.right)) + 1
}

之后是否平衡就比较好求了，首先比较直接子节点 left 和 right 是否高度相差绝对值 <= 1，之后再递归的比较 left 和 right 是否是平衡二叉树即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isBalanced = function (root) {
  if (!root) {
    return true
  }
  let isSonBalanced =
    Math.abs(getHeight(root.left) - getHeight(root.right)) <= 1
  return isSonBalanced && isBalanced(root.left) && isBalanced(root.right)
}

路径总和-112

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:

给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

思路

从第一个节点求是否有路径之和为 22，可以转化为从左节点开始，是否有路径之和为 22 -5 = 18，也可以转化为从右节点开始，是否有路径之和为 22 - 5 = 18。

当递归调用函数时，发现节点没有左右子节点，说明它是叶子节点，此时就可以对比当前的值是否和传入的目标值 sum 相等，返回结果即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function (root, targetSum) {
  if (!root) {
    return false
  }
  // 叶子节点，判断当前的信息是否等于sum即可
  if (!root.left && !root.right) {
    return root.val === targetSum
  }
  return (
    hasPathSum(root.left, targetSum - root.val) ||
    hasPathSum(root.right, targetSum - root.val)
  )
}

左叶子之和-404

计算给定二叉树的所有左叶子之和。

示例：

    3
   / \
  9  20
    /  \
   15   7

在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/sum-of-left-leaves 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

用 DFS 的思路，去递归的判断目标节点的左节点是否是叶子节点，如果是的话，就把全局的 sum 加上目标节点的值。然后继续 DFS 目标节点的左右子节点。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumOfLeftLeaves = function (root) {
  let sum = 0
  let dfs = (node) => {
    if (!node) return
    if (isLeaf(node.left)) {
      sum += node.left.val
    }
    dfs(node.left)
    dfs(node.right)
  }
  dfs(root)
  return sum
}

function isLeaf(node) {
  return !!node && !node.left && !node.right
}

二叉树的所有路径-257

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

输入:

   1
 /   \
2     3
 \
  5

输出: ["1->2->5", "1->3"]

解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/binary-tree-paths 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

给递归函数传递一个 path 数组，记录当前位置已经走过的节点，如果是叶子节点的话，就可以往全局的 res 结果数组里增加一个结果。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function (root) {
  let res = []
  let dfs = (node, path = '') => {
    if (!node) {
      return
    }
    let newPath = path ? `${path}->${node.val}` : `${node.val}`
    if (!node.left && !node.right) {
      res.push(newPath)
    }
    dfs(node.left, newPath)
    dfs(node.right, newPath)
  }
  dfs(root)
  return res
}

路径总和 II-113

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1
返回:

[
   [5,4,11,2],
   [5,8,4,5]
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/path-sum-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

典型的可以用 DFS 来解决的问题，定义一个 search 方法并且参数里带一个用来收集路径的 paths 数组，每当到达叶子节点（没有 left 也没有 right），就计算一把路径的总和，如果等于目标值就 push 到结果数组里。（注意这里要浅拷贝一下，防止下面的计算污染这个数组）

任何一个节点处理完成时，都要把当前节点 pop 出 paths 数组。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number[][]}
 */
var pathSum = function (root, targetSum) {
  let res = []
  let search = function (node, paths) {
    if (isInvalid(node)) {
      return
    }
    paths.push(node.val)
    if (node.left) {
      search(node.left, paths)
    }
    if (node.right) {
      search(node.right, paths)
    }
    if (!node.left && !node.right) {
      if (sumVals(paths) === targetSum) {
        res.push(paths.slice())
      }
    }
    paths.pop()
  }
  search(root, [])
  return res
}

function sumVals(nodes) {
  return nodes.reduce((prev, val) => {
    prev += val
    return prev
  }, 0)
}

function isInvalid(node) {
  return !node || node.val === undefined || node.val === null
}

求根到叶子节点数字之和-129

给定一个二叉树，它的每个结点都存放一个 0-9 的数字，每条从根到叶子节点的路径都代表一个数字。

例如，从根到叶子节点路径 1->2->3 代表数字 123。

计算从根到叶子节点生成的所有数字之和。

说明: 叶子节点是指没有子节点的节点。

示例 1:

输入: [1,2,3]
    1
   / \
  2   3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此，数字总和 = 12 + 13 = 25.

示例 2:

输入: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
输出: 1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495.
从根到叶子节点路径 4->9->1 代表数字 491.
从根到叶子节点路径 4->0 代表数字 40.
因此，数字总和 = 495 + 491 + 40 = 1026.

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/sum-root-to-leaf-numbers 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

先按照字符串拼接的思路用 DFS 收集所有到达叶子节点的路径的集合，最后把这些字符串转化为数字求和即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumNumbers = function (root) {
  let paths = []
  let dfs = (node, path) => {
    if (!node) {
      return
    }
    let newPath = `${path}${node.val}`
    if (!node.left && !node.right) {
      paths.push(newPath)
      return
    }
    dfs(node.left, newPath)
    dfs(node.right, newPath)
  }
  dfs(root, '')
  return paths.reduce((total, val) => {
    return total + Number(val)
  }, 0)
}

路径总和 III-437

给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过 1000 个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

返回 3。和等于 8 的路径有:

1.  5 -> 3
2.  5 -> 2 -> 1
3.  -3 -> 11

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/path-sum-iii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这是一道被吐槽难度的 easy 题，递归的思路有点难找。

实际上这题需要统计三个值：

1. 以 node 为起点，包含这个 node 本身加起来等于 sum 的路径数量之和。
2. 以 node.left 为起点，等于 sum 的路径数量之和。
3. 以 node.right 为起点，等于 sum 的路径数量之和。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function (root, targetSum) {
  if (!root) return 0
  return (
    countSum(root, targetSum) +
    pathSum(root.left, targetSum) +
    pathSum(root.right, targetSum)
  )
}

let countSum = (node, sum) => {
  let count = 0
  let dfs = (node, target) => {
    if (!node) return

    // 这里拿到结果不能直接return，要继续向下考虑
    // 比如下面的两个节点 1,-1 那么它们相加得0 也能得到一个路径
    if (node.val === target) {
      count += 1
    }
    dfs(node.left, target - node.val)
    dfs(node.right, target - node.val)
  }
  dfs(node, sum)
  return count
}

二叉搜索树的最近公共祖先 -235

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

链接

算法思路

1. 利用二叉搜索树的性质：
   • 如果节点 p 和 q 的值都小于当前节点的值，说明它们都在当前节点的左子树，递归左子树。
   • 如果节点 p 和 q 的值都大于当前节点的值，说明它们都在当前节点的右子树，递归右子树。
   • 如果一个节点的值介于 p 和 q 之间（或当前节点就是 p 或 q），那么当前节点就是最近公共祖先。
2. 终止条件：
   • 找到最近公共祖先节点时停止递归。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  if (!root) return null

  // 如果p和q都小于root，递归左子树
  if (p.val < root.val && q.val < root.val) {
    return lowestCommonAncestor(root.left, p, q)
  }

  // 如果p和q都大于root，递归右子树
  if (p.val > root.val && q.val > root.val) {
    return lowestCommonAncestor(root.right, p, q)
  }

  // 否则，当前节点就是最近公告祖先
  return root
}

验证二叉搜索树-98

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左

  子树

  只包含

  小于

  当前节点的数。

• 节点的右子树只包含 大于 当前节点的数。

• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

链接

思路

1. 定义约束条件：
   • 一个节点的值必须满足当前的上下界条件： low < node.val < high
   • 对于左子树：high 更新为当前节点值。
   • 对于右子树：low 更新为当前节点值。
2. 递归判断：
   • 递归检查左子树和右子树是否满足上述条件。
   • 如果某个节点不满足条件，立即返回 false。
3. 终止条件：
   • 空节点返回 true，因为空树是有效的二叉搜索树。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  const validate = (node, low, high) => {
    if (!node) return true // 空节点，直接有效
    if (node.val <= low || node.val >= high) return false // 不满足条件

    // 递归检查左右子树
    return (
      validate(node.left, low, node.val) && validate(node.right, node.val, high)
    )
  }

  return validate(root, -Infinity, Infinity) // 初始上下界为无穷大
}

删除二叉搜索树中的节点-450

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点； 如果找到了，删除它。 说明： 要求算法时间复杂度为 O(h)，h 为树的高度。

示例:

root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7

给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。

一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。

    5
   / \
  4   6
 /     \
2       7

另一个正确答案是 [5,2,6,null,4,null,7]。

    5
   / \
  2   6
   \   \
    4   7

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/delete-node-in-a-bst
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题我的思路是这样的，先通过递归去找到目标节点的 父节点 parent，和目标节点的位置 pos：left 或 right，方便后续删除操作。

1. 待删除节点没有 left或者 right 子节点的情况下，直接吧 parent[pos] = null 清空即可。
2. 待删除节点只有 left 或只有 right，那就把 parent[pos] 赋值为存在的那个子节点即可。
3. 如果 left 和 right 都在的情况下，比较复杂一些，把待删除节点的左右子节点分别称为 targetLeft 和 targetRight，先找到targetRight的最左子节点，这个子节点一定在右子树中最小，但是在左子树中最大。然后把 parent[pos] 赋值为 targetRight，再把 targetRight的最左下角子节点的 left 赋值成原来的 targetLeft 即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} key
 * @return {TreeNode}
 */
var deleteNode = function (root, key) {
  let findNodePos = (node, key) => {
    if (!node) {
      return false
    }
    if (node.left && node.left.val === key) {
      return {
        parent: node,
        pos: 'left'
      }
    } else if (node.right && node.right.val === key) {
      return {
        parent: node,
        pos: 'right'
      }
    } else {
      return findNodePos(node.left, key) || findNodePos(node.right, key)
    }
  }

  let findLastLeft = (node) => {
    if (!node.left) {
      return node
    }
    return findLastLeft(node.left)
  }

  let virtual = new TreeNode()
  virtual.left = root

  let finded = findNodePos(virtual, key)
  if (finded) {
    let { parent, pos } = finded
    let target = parent[pos]
    let targetLeft = target.left
    let targetRight = target.right

    if (!targetLeft && !targetRight) {
      parent[pos] = null
    } else if (!targetRight) {
      parent[pos] = targetLeft
    } else if (!targetLeft) {
      parent[pos] = targetRight
    } else {
      parent[pos] = targetRight
      let lastLeft = findLastLeft(targetRight)
      lastLeft.left = targetLeft
    }
  }

  return virtual.left
}

将有序数组转换为二叉搜索树-108

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

将有序数组分为左、中、右三个部分，以中为根节点，并且递归的对左右两部分建立平衡二叉树即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
let sortedArrayToBST = function (nums) {
  let n = nums.length
  if (!n) {
    return null
  }
  let mid = Math.floor(n / 2)
  let root = new TreeNode(nums[mid])

  root.left = sortedArrayToBST(nums.slice(0, mid))
  root.right = sortedArrayToBST(nums.slice(mid + 1, n))

  return root
}

二叉搜索树中第 K 小的元素-230

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

链接

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function (root, k) {
  let count = 0
  let result = null

  const inorder = (node) => {
    if (!node) return

    // 左子树
    inorder(node.left)

    // 当前节点
    count++
    if (count === k) {
      result = node.val
      return // 找到目标，提前终止
    }

    // 右子树
    inorder(node.right)
  }

  inorder(root)
  return result
}

二叉树的最近公共祖先-236

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。 示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉树中。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

先通过 DFS 去找到 p 和 q 节点的深度，并且在查找的过程中对节点和他们的子节点之间建立父子关系。

之后，从深度最浅的那个节点开始（深度浅，离公共祖先一定更近）不断往上查找公共祖先即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  let findAndCreate = (node, target, depth) => {
    if (node !== target) {
      let findInLeft
      if (node.left) {
        node.left.parent = node
        findInLeft = findAndCreate(node.left, target, depth + 1)
      }

      if (findInLeft) {
        return findInLeft
      } else {
        if (node.right) {
          node.right.parent = node
          return findAndCreate(node.right, target, depth + 1)
        }
      }
    } else {
      return {
        depth,
        node
      }
    }
  }

  let findP = findAndCreate(root, p, 0) || {}
  let findQ = findAndCreate(root, q, 0) || {}

  let cur = findP.depth > findQ.depth ? findQ.node : findP.node

  while (!(isAncestor(cur, p) && isAncestor(cur, q))) {
    cur = cur.parent
  }

  return cur
}

function isAncestor(node, target) {
  if (!node) {
    return false
  }
  if (node !== target) {
    return !!(isAncestor(node.left, target) || isAncestor(node.right, target))
  } else {
    return true
  }
}

思路

1. 递归定义：
   • 如果当前节点为空，返回 null。
   • 如果当前节点等于 p 或 q，返回当前节点。
   • 递归查找左子树和右子树：
     • 如果左子树和右子树的递归结果都不为空，则当前节点是最近公共祖先。
     • 如果其中一个为空，返回另一个（可能是最近公共祖先）。
2. 核心思想：
   • 利用二叉树的递归性质。
   • 如果 p 和 q 分别位于左右子树，则当前节点是它们的最近公共祖先。
   • 如果 p 和 q 都在一侧，递归会返回最近公共祖先。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  // 如果当前节点为空，或等于 p 或 q，则返回当前节点
  if (!root || root === p || root === q) return root

  // 递归查找左子树和右子树
  let left = lowestCommonAncestor(root.left, p, q)
  let right = lowestCommonAncestor(root.right, p, q)

  // 如果左右子树都不为空，说明当前节点是最近公共祖先
  if (left && right) return root

  // 否则返回非空的那个
  return left || right
}

电话号码的字母组合-17

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

思路

每次递归中都对当前数字所代表的的字母全部列出来，拼在已完成的字符后面，再交给下一次递归。通过 index 下标来判断是否完成，一旦长度符合，就放入结果数组中。

/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function (digits) {
  let res = []

  if (digits === '') {
    return res
  }

  let findCombinations = (index, str) => {
    if (digits.length === index) {
      res.push(str)
      return
    }

    let char = digits[index]
    let letters = letterMap[Number(char)]

    for (let i = 0; i < letters.length; i++) {
      let letter = letters[i]
      findCombinations(index + 1, `${str}${letter}`)
    }
  }

  findCombinations(0, '')

  return res
}

let letterMap = [
  ' ', //0
  '', //1
  'abc', //2
  'def', //3
  'ghi', //4
  'jkl', //5
  'mno', //6
  'pqrs', //7
  'tuv', //8
  'wxyz' //9
]

复原IP地址-93

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成），整数之间用 '.' 分隔。

示例:

输入: "25525511135"
输出: ["255.255.11.135", "255.255.111.35"]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/restore-ip-addresses
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

利用一个辅助的 DFS函数，每次可以传入当前起始的位置，和当前已使用的.的数量，然后通过范围在 1 ~ 3 来继续分割出不同的下一位ip地址。

当.的使用数到达3的时候，就直接判断剩余的字符是否满足ip条件，满足的放入数组即可。

这题本身并不难，但是边界情况比较多。比如说如果分割出来的一块地址开头是0的话，那么必须只有一位，也就是 0，而不能是 01或者001这种。

/**
 * @param {string} s
 * @return {string[]}
 */
let restoreIpAddresses = function (s) {
  let res = []
  let findPos = (start, prev, used) => {
    if (used === 3) {
      let rest = s.substr(start)
      // 点全部用光后 剩余字符依然是一个合格的ip chunk
      // 就视为一个答案 放入数组
      if (isValidChunk(rest)) {
        res.push(prev.concat(rest).join('.'))
      }
      return
    }

    for (let i = 1; i <= 3; i++) {
      let end = start + i
      let cur = s.substring(start, end)
      if (isValidChunk(cur)) {
        findPos(end, prev.concat(cur), used + 1)
      }
    }
  }

  findPos(0, [], 0)

  return res
}

function isValidChunk(str) {
  let strLen = str.length
  if (strLen === 0) {
    return false
  }
  // 开头是0的话 只能整个字符串只有一位0才行
  if (str[0] === '0') {
    return strLen === 1
  }
  let num = Number(str)
  return num <= 255
}

分割回文串-131

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例:

输入: "aab"
输出:
[
  ["aa","b"],
  ["a","a","b"]
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/palindrome-partitioning 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

递归全排列

尝试所有的下标做起点，所有的下标作为终点，递归暴力判断。

/**
 * @param {string} s
 * @return {string[][]}
 */
var partition = function (s) {
  let n = s.length
  let ret = []
  let find = function (start, prev) {
    // 最长分个一个字符，最多分割到末尾前一位
    for (let i = 1; i <= n; i++) {
      let end = start + i
      let cur = s.substring(start, end)
      if (cur) {
        let res = prev.concat(cur)
        if (isPalindrome(cur)) {
          if (end === n) {
            ret.push(res)
          } else {
            find(start + i, res)
          }
        }
      }
    }
  }
  find(0, [])
  return ret
}

function isPalindrome(s) {
  if (!s) {
    return false
  }
  let i = 0
  let j = s.length - 1

  while (i < j) {
    let head = s[i]
    let tail = s[j]

    if (head !== tail) {
      return false
    } else {
      i++
      j--
    }
  }
  return true
}

全排列-46

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/permutations 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

把排列的问题分治为小问题，由小问题的递归推断出最后的解。

[1, 2] 可以分割为 1 和 permute([2]) 的所有组合，也可以分割为 2 和 permute([1])的所有组合。

[1, 2, 3] 可以分割为 3 和 permute([1, 2]) 的所有组合（上一步已经求得），也可以分为 2 和 permute([1, 3])的所有组合，以此类推。

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
  let n = nums.length
  if (n === 1) {
    return [nums]
  }

  let res = []
  for (let i = 0; i < n; i++) {
    let use = nums[i]
    let rest = nums.slice(0, i).concat(nums.slice(i + 1, n))
    let restPernuteds = permute(rest)
    for (let restPernuted of restPernuteds) {
      res.push(restPernuted.concat(use))
    }
  }

  return res
}

全排列 II-47

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

输入: [1,1,2]
输出:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/permutations-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

本题和全排列-46的思路是一样的，只是在每次递归保存的时候，利用 Set 去重的特性，把每个值用字符串拼接的方式丢进 set 里去重，最后再处理成题目需要的格式即可。

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let uniqSymbol = 'X'

let permuteUnique = function (nums) {
  let n = nums.length
  if (n === 1) {
    return [nums]
  }
  let permuteSet = (nums) => {
    let n = nums.length
    if (n === 0) {
      return new Set()
    }
    if (n === 1) {
      return new Set(nums)
    }

    let res = new Set()
    for (let i = 0; i < n; i++) {
      let use = nums[i]
      if (use === undefined) {
        continue
      }
      let rest = nums.slice(0, i).concat(nums.slice(i + 1, n))
      let restPermuteds = permuteSet(rest)
      restPermuteds.forEach((restPermuted) => {
        res.add(`${use}${uniqSymbol}${restPermuted}`)
      })
    }

    return res
  }

  let permuted = permuteSet(nums)

  return Array.from(permuted).map((val) => val.split(uniqSymbol).map(Number))
}

组合-77

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/combinations 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

定义一个 helper 函数，递归的时候接受本次处理的 start 起始位置，和上一次已经取了字符后得到的 prev 数组。继续进一步的循环递归，增加 start 和拼接 prev 即可。

当 prev 的长度等于 k 时，条件满足，把当前的 prev 存入结果数组中。

/**
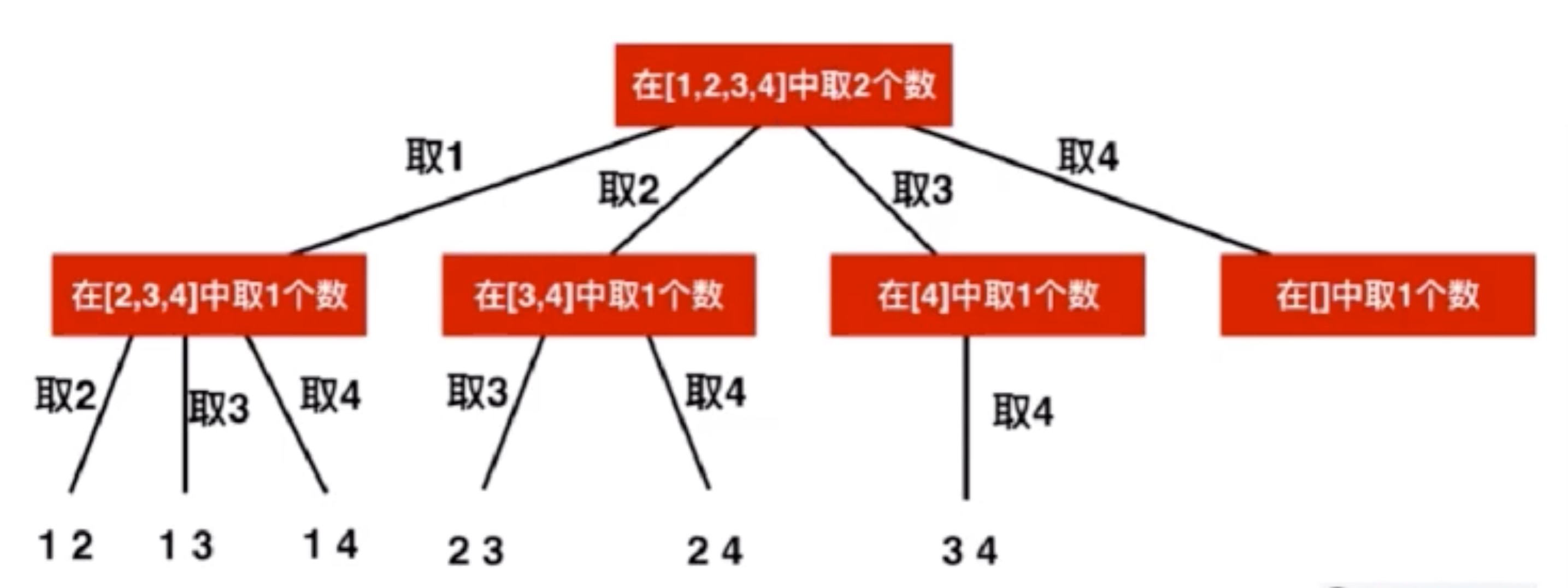
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function (n, k) {
  let ret = []

  let helper = (start, perv) => {
    let len = perv.length
    if (len === k) {
      ret.push(perv)
      return
    }

    if (start > n) {
      return
    }

    for (let i = start; i <= n; i++) {
      helper(i + 1, perv.concat(i))
    }
  }

  helper(1, [])
  return ret
}

剪枝

在循环中，要考虑当前已经凑成的数组长度和剩下的数字所能凑成的最大长度，对于不可能凑成的情况直接 continue。

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function (n, k) {
  let ret = []

  let helper = (start, perv) => {
    let len = perv.length
    if (len === k) {
      ret.push(perv)
      return
    }

    if (start > n) {
      return
    }

    // 还有rest个位置待填补
    let rest = k - perv.length
    for (let i = start; i <= n; i++) {
      if (n - i + 1 < rest) {
        continue
      }
      helper(i + 1, perv.concat(i))
    }
  }

  helper(1, [])
  return ret
}

组合总和-39

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。 解集不能包含重复的组合。

示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]
示例 2:

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/combination-sum 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题乍一看很难，因为有重复元素，相对于之前的几道题来说引入了新的概念。

但是其实仔细想一下，之前的递归，我们对于 helper 递归函数每次递归都会把 start 起点 +1，如果我们每次递归不去 +1，而是把 start也考虑在内的话，是不是就可以把重复元素的情况也考虑进去了呢？

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
  let res = []

  let helper = (start, prevSum, prevArr) => {
    // 由于全是正整数，所以一旦和大于目标值了，直接结束本次递归即可
    if (prevSum > target) {
      return
    }
    // 目标值达成
    if (prevSum === target) {
      res.push(prevArr)
      return
    }

    for (let i = start; i < candidates.length; i++) {
      // 这里还是继续从start本身开始，因为多个重复值是允许的
      let cur = candidates[i]
      let sum = prevSum + cur
      let arr = prevArr.concat(cur)
      helper(i, sum, arr)
    }
  }

  helper(0, 0, [])
  return res
}

组合总和 II-40

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。 解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]
示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/combination-sum-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

和组合总和-39思路类似，只不过由于不需要考虑同一个元素重复使用的情况，每次的递归的 start 起点应该是 prevStart + 1。

由于数组中可能出现多个相同的元素，他们有可能会生成相同的解，比如 [1, 1, 7] 去凑 8 的时候，可能会用下标为 0 的 1 和 7 去凑 8，也可能用下标为 1 的 1 和 7 去凑 8。

所以在把解放入数组中之前，需要先通过一个唯一的 key 去判断这个解是否生成过，但是考虑到 [1, 2, 1, 2, 7] 这种情况去凑 10，可能会生成 [1, 2, 7] 和 [2, 1, 7] 这样顺序不同但是结果相同的解，这是不符合题目要求的。

所以一个简单的方法就是，先把数组排序后再求解，这样就不会出现顺序不同的相同解了，此时只需要做简单的数组拼接即可生成 key [1, 2, 7] -> "1 ~ 2 ~ 7"。

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function (candidates, target) {
  let res = []
  let path = []
  let total = 0
  candidates.sort((a, b) => a - b)
  let used = new Array(candidates.length).fill(false)
  let helper = (start) => {
    if (total > target) return
    if (total === target) {
      res.push([...path])
      return
    }
    for (let i = start; i < candidates.length; i++) {
      if (used[i - 1] === false && candidates[i - 1] === candidates[i]) continue
      used[i] = true
      total += candidates[i]
      path.push(candidates[i])
      helper(i + 1)
      path.pop()
      used[i] = false
      total -= candidates[i]
    }
  }
  helper(0)
  return res
}

组合总和 III-216

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。 解集不能包含重复的组合。 示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/combination-sum-iii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

简单的套前面几道递归回溯题的模板即可完成，注意剪枝条件，由于全部的值都是正整数，所以当和大于目标值的时候，但是数组长度还小于目标长度的话，可以直接 return。

/**
 * @param {number} k
 * @param {number} n
 * @return {number[][]}
 */
var combinationSum3 = function (k, n) {
  let res = []

  let helper = (start, prevSum, prev) => {
    if (prev.length === k && prevSum === n) {
      res.push(prev)
      return
    }

    if (prevSum > n) {
      return
    }

    for (let i = start + 1; i <= 9; i++) {
      helper(i, prevSum + i, prev.concat(i))
    }
  }

  helper(0, 0, [])
  return res
}

子集-78

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/subsets 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

求子集，其实可以转化为在数组中，求长度从 1 ~ nums.length 的每种长度下的全部组合。

那么定义 helper 函数，接受的参数为 start 起点， prev 之前拼成的数组，targetLength 目标长度。在这个递归过程中，目标长度是不变的。只需要 prev 的长度和 targetLength 相等，即可完成一个结果放入 res 数组中。

最后，针对 targetLength 为 1 ~ nums.length ，分别调用 helper 函数即可：

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function (nums) {
  let res = []
  let n = nums.length
  if (n === 0) {
    return res
  }

  let helper = (start, prev, targetLength) => {
    if (start > n) {
      return
    }
    if (prev.length === targetLength) {
      res.push(prev)
      return
    }

    for (let i = start; i < n; i++) {
      let cur = nums[i]
      helper(i + 1, prev.concat(cur), targetLength)
    }
  }

  for (let j = 1; j <= nums.length; j++) {
    helper(0, [], j)
  }

  return [[], ...res]
}

子集 II-90

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/subsets-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

本题和 组合总和 II-40 的思路类似，剪枝的思路也是和之前相似的，如果循环的时候发现剩余的数字不足以凑成目标长度，就直接剪掉。

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsetsWithDup = function (nums) {
  let n = nums.length
  let res = []
  if (!n) {
    return res
  }

  nums.sort()

  let used = {}

  let helper = (start, prev, target) => {
    if (prev.length === target) {
      let key = getKey(prev)
      if (!used[key]) {
        res.push(prev)
        used[key] = true
      }
      return
    }

    for (let i = start; i < n; i++) {
      let rest = n - i
      let need = target - prev.length
      if (rest < need) {
        continue
      }
      helper(i + 1, prev.concat(nums[i]), target)
    }
  }

  for (let i = 1; i <= n; i++) {
    helper(0, [], i)
  }

  return [[], ...res]
}

function getKey(arr) {
  return arr.join('~')
}

二进制手表-401

二进制手表顶部有 4 个 LED 代表 小时（0-11），底部的 6 个 LED 代表 分钟（0-59）。

每个 LED 代表一个 0 或 1，最低位在右侧。

例如，上面的二进制手表读取 “3:25”。

给定一个非负整数 n 代表当前 LED 亮着的数量，返回所有可能的时间。

示例：

输入: n = 1
返回: ["1:00", "2:00", "4:00", "8:00", "0:01", "0:02", "0:04", "0:08", "0:16", "0:32"]

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/binary-watch 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题真的没感觉是 easy 难度的题型，更像是前面几个递归题目的综合考察版本。

首先拆解开来看，对于分钟和时钟，我们有一个通用的需求就是求出在剩余的亮起的点的数量在 n 时，求可能的所有排列组合。

具体点说，我们要实现的 combine 函数是这样的：时钟有 [1, 2, 4, 8] 四种可能性，在亮起点数为 1 时，它的所有求和的可能性是 [1, 2, 4, 8]，在亮起点数为 2 时，它的可能性就变成了 [1 + 2, 1 + 4, 1 + 8, 2 + 4, 2 + 8, 4 + 8] 以此类推。

假设给你的总亮点数是 2，那么：

• 你可以分配给时钟 0 个点，剩下的 2 个点就分配给分钟。也就是求 combine(hours, 0) 和 combine(minutes, 2) 的笛卡尔积。
• 你可以分配给时钟 1 个点，剩下的 1 个点就分配给分钟。也就是求 combine(hours, 1) 和 combine(minutes, 1) 的笛卡尔积。
• 你可以分配给时钟 2 个点，剩下的 0 个点就分配给分钟。也就是求 combine(hours, 2) 和 combine(minutes, 0) 的笛卡尔积。

有了这个思路，其实核心部分就是实现 combine 函数了，并且注意要对时钟和分钟进行一个异常数值的校验，对分钟进行一个补零的拼接：

/**
 * @param {number} num
 * @return {string[]}
 */
let HOURS = [1, 2, 4, 8]
let MINUTES = [1, 2, 4, 8, 16, 32]

let readBinaryWatch = function (num) {
  let res = []

  let combine = (arr, num) => {
    if (num === 0) {
      return [0]
    }
    let res = []
    let helper = (start, prevCount, prevSum) => {
      if (prevCount === num) {
        res.push(prevSum)
        return
      }

      for (let i = start; i < arr.length; i++) {
        let cur = arr[i]
        helper(i + 1, prevCount + 1, prevSum + cur)
      }
    }
    helper(0, 0, 0)
    return res
  }

  for (let i = 0; i <= num; i++) {
    let hours = combine(HOURS, i)
    let minutes = combine(MINUTES, num - i)

    for (let hour of hours) {
      if (hour > 11) continue
      for (let minute of minutes) {
        if (minute > 59) {
          continue
        }
        res.push(`${hour}:${padLeft(minute)}`)
      }
    }
  }
  return res
}

function padLeft(num) {
  let str = num.toString()
  if (str.length === 1) {
    str = `0${str}`
  }
  return str
}

单词搜索-79

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/word-search 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这是一个比较经典的可以用递归回溯法来解决的二维数组问题，这里用到几个技巧：

1. 用 [[-1, 0], [1, 0], [0, -1], [0, 1]] 这样的数组来标记访问 左、右、上、下 位置需要偏移的坐标量。
2. 用和目标数组结构完全一致的二维数组 visited 来标记已访问过的元素，防止在递归的过程中重复访问，陷入死循环。
3. 用一个 inArea 函数来判断接下来要访问的元素是否超出整个二维数组的边界。

递归函数

有了这些辅助方法后，接下来就需要创建一个递归函数 search，它接受的参数为：

1. startX：本次匹配字符的起始 X 坐标。
2. startY：本次匹配字符的起始 Y 坐标。
3. wordIndex：本次需要匹配的字符串下标，在前一个下标已经成功匹配后才会进一步累加。

在这个递归函数中，如果当前的 x、y 在二维数组中对应的字符和 wordIndex 所对应的字符匹配一致的话，并且 wordIndex 还没有到字符串的最后一位的话，就继续递归的向 上、下、左、右四个方向进一步递归匹配字符串的下一个下标 wordIndex + 1即可。

当 wordIndex 成功的来到字符串的最后一位下标后，即可根据最后一位字符是否匹配当前的 x、y 来决定本次整个递归的返回值。

主函数

主函数中，只需要遍历整个二维数组，不断的以当前的坐标和 wordIndex = 0 开始从第一个字符遍历，只要 search 函数返回 true，就说明匹配成功，整体返回 true 结果即可。

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
let directions = [
  [-1, 0],
  [1, 0],
  [0, -1],
  [0, 1]
] // 左右上下
var exist = function (board, word) {
  let maxY = board.length
  if (!maxY) return false
  let maxX = board[0].length

  // 二维数组记录已访问过的元素
  let visited = new Array(maxY)
  for (let y = 0; y < visited.length; y++) {
    visited[y] = new Array(maxX)
  }

  let inArea = (x, y) => {
    return x >= 0 && x < maxX && y >= 0 && y < maxY
  }

  let search = (startX, startY, wordIndex) => {
    // 当前起始字符不匹配，直接失败
    let curCell = board[startY][startX]
    let curChar = word[wordIndex]
    if (curCell !== curChar) {
      return false
    }

    // 如果递归到最后一个字符，就直接返回最后一个字符是否匹配成功
    if (wordIndex === word.length - 1) {
      return curChar === curChar
    }

    // 进一步递归，先记录为已访问元素，防止递归的时候重复访问
    visited[startY][startX] = true

    for (let direction of directions) {
      let [x, y] = direction
      let nextX = startX + x
      let nextY = startY + y

      // 需要保证未越界且被访问过
      if (inArea(nextX, nextY) && !visited[nextY][nextX]) {
        if (search(nextX, nextY, wordIndex + 1)) {
          return true
        }
      }
    }
    // 充值已访问标记位
    visited[startY][startX] = false
  }

  for (let y = 0; y < maxY; y++) {
    for (let x = 0; x < maxX; x++) {
      if (search(x, y, 0)) {
        return true
      }
    }
  }

  return false
}

岛屿数量-200

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

链接

思路

1. 定义岛屿：
   • 连续的 '1'（陆地）组成一个岛屿，只有水平或垂直相邻的 '1' 才能连接。
   • 遇到一个未访问的 '1'，通过 DFS 或 BFS 将其所有相邻的 '1' 标记为访问过。
2. 遍历网格：
   • 遍历整个网格，当遇到 '1' 时，触发 DFS 或 BFS，将整个岛屿淹没（即将所有相邻的 '1' 变为 '0'）。
   • 每触发一次 DFS/BFS，岛屿数量 +1。
3. 优化：
   • 修改原网格作为标记访问的方法，避免额外的空间开销。

/**
 * @param {character[][]} grid
 * @return {number}
 */
var numIslands = function (grid) {
  if (!grid || grid.length === 0) return 0

  const rows = grid.length
  const cols = grid[0].length
  let count = 0

  const dfs = (i, j) => {
    // 边界条件：超出网格范围或遇到水
    if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] === '0') return

    // 标记当前陆地为访问过
    grid[i][j] = '0'

    // 递归访问上下左右
    dfs(i - 1, j)
    dfs(i + 1, j)
    dfs(i, j - 1)
    dfs(i, j + 1)
  }

  // 遍历整个网格
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (grid[i][j] === '1') {
        count++ // 每发现一个新的岛屿，计数+1
        dfs(i, j) // 淹没整个岛屿
      }
    }
  }

  return count
}

被围绕的区域-130

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获 所有 被围绕的区域：

• **连接：**一个单元格与水平或垂直方向上相邻的单元格连接。
• 区域：连接所有 'O' 的单元格来形成一个区域。
• **围绕：**如果您可以用 'X' 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

通过将输入矩阵 board 中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。

示例 1：

**输入：**board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]

输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]

解释：

在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

**输入：**board = [["X"]]

输出：[["X"]]

链接

思路

只需要遍历四个边界上的节点，遇到 O 的边界点才开始蔓延遍历，并且把遍历到的节点都标记为 #（防止重复遍历）.。最后再一次性遍历整个二维数组，遇到 # 标记的格子都转为 O（因为是从边界蔓延的，一定是不符合 X 的条件的）。

1. 边缘扩展的标记法：
   • 从矩阵边界的 'O' 开始，进行深度优先搜索（DFS）或广度优先搜索（BFS），将与边界相连的所有 'O' 标记为特殊字符（如 '#'）。
   • 这些 'O' 是未被围绕的区域。
2. 遍历整个矩阵：
   • 将剩余的 'O' 替换为 'X'，因为它们是被围绕的区域。
   • 将特殊字符 '#' 恢复为 'O'，因为它们是未被围绕的区域。
3. 优化：
   • 使用原地修改，避免额外空间开销。

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
var solve = function (board) {
  if (!board || board.length === 0 || board[0].length === 0) return

  const rows = board.length
  const cols = board[0].length

  // 深度优先搜索，标记未被围绕的区域
  const dfs = (i, j) => {
    if (i < 0 || i >= rows || j < 0 || j >= cols || board[i][j] !== 'O') return
    board[i][j] = '#' // 标记为未被围绕
    dfs(i - 1, j)
    dfs(i + 1, j)
    dfs(i, j - 1)
    dfs(i, j + 1)
  }

  // 标记边缘的 'O' 和与之相连的区域
  for (let i = 0; i < rows; i++) {
    dfs(i, 0) // 左边界
    dfs(i, cols - 1) // 右边界
  }
  for (let j = 0; j < cols; j++) {
    dfs(0, j) // 上边界
    dfs(rows - 1, j) // 下边界
  }

  // 遍历整个矩阵，修改内容
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (board[i][j] === 'O') {
        board[i][j] = 'X' // 被围绕的区域
      } else if (board[i][j] === '#') {
        board[i][j] = 'O' // 恢复未被围绕的区域
      }
    }
  }
}

太平洋大西洋水流问题-417

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

链接

思路

1. 从边界开始反向流动：
   • 分别从太平洋和大西洋的边界出发进行深度优先搜索（DFS）或广度优先搜索（BFS），标记能够从这些边界流入的单元格。
   • 太平洋的边界：第一行和第一列。
   • 大西洋的边界：最后一行和最后一列。
2. 交集：
   • 两个标记结果的交集就是既能流向太平洋又能流向大西洋的单元格。

/**
 * @param {number[][]} heights
 * @return {number[][]}
 */
var pacificAtlantic = function (heights) {
  const rows = heights.length
  const cols = heights[0].length
  const pacific = Array.from({ length: rows }, () => Array(cols).fill(false))
  const atlantic = Array.from({ length: rows }, () => Array(cols).fill(false))

  const dfs = (row, col, ocean) => {
    ocean[row][col] = true
    const directions = [
      [-1, 0],
      [1, 0],
      [0, -1],
      [0, 1] // 上下左右
    ]
    for (const [dr, dc] of directions) {
      const newRow = row + dr
      const newCol = col + dc
      if (
        newRow >= 0 &&
        newRow < rows &&
        newCol >= 0 &&
        newCol < cols &&
        !ocean[newRow][newCol] &&
        heights[newRow][newCol] >= heights[row][col] // 确保水能反向流动
      ) {
        dfs(newRow, newCol, ocean)
      }
    }
  }

  // 从太平洋边界开始流动
  for (let i = 0; i < rows; i++) {
    dfs(i, 0, pacific) // 第一列
    dfs(i, cols - 1, atlantic) // 最后一列
  }
  for (let j = 0; j < cols; j++) {
    dfs(0, j, pacific) // 第一行
    dfs(rows - 1, j, atlantic) // 最后一行
  }

  // 找到既能流向太平洋又能流向大西洋的单元格
  const result = []
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (pacific[i][j] && atlantic[i][j]) {
        result.push([i, j])
      }
    }
  }
  return result
}

N皇后-51

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

提示：

皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一到七步，可进可退。（引用自 百度百科 - 皇后 ）

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/n-queens 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

其实这题虽然是 hard 问题，但是思路比较清晰，还是通过递归不断的根据上一行摆放的结果去找下一行可以摆放的位置，递归进行下去，直到最后一行得出结果。

但是这题的难点在于判断的手法比较复杂，当前一行已经落下一个皇后之后，下一行需要判断三个条件：

1. 在这一列上，之前不能摆放过皇后。
2. 在对角线 1，也就是「左下 -> 右上」这条对角线上，之前不能摆放过皇后。
3. 在对角线 2，也就是「右上 -> 左下」这条对角线上，之前不能摆放过皇后。

难点在于判断对角线上是否摆放过皇后了，其实找到规律后也不难了，看图：

对角线1：

直接通过这个点的横纵坐标 rowIndex + columnIndex 相加，相等的话就在同在对角线 1 上：

对角线2：

直接通过这个点的横纵坐标 rowIndex - columnIndex 相减，相等的话就在同在对角线 2 上：

所以：

1. 用 columns 数组记录摆放过的列下标，摆放过后直接标记为 true 即可。
2. 用 dia1 数组记录摆放过的对角线1下标，摆放过后直接把下标 rowIndex + columnIndex标记为 true 即可。
3. 用 dia2 数组记录摆放过的对角线1下标，摆放过后直接把下标 rowIndex - columnIndex标记为 true 即可。
4. 递归函数的参数 row 代表每一行中皇后放置的列数，比如 row[0] = 3 代表第 0 行皇后放在第 3 列，以此类推。
5. 每次进入递归函数前，先把当前项所对应的列、对角线1、对角线2的下标标记为 true，带着标记后的状态进入递归函数。并且在退出本次递归后，需要把这些状态重置为 false ，再进入下一轮循环。

有了这几个辅助知识点，就可以开始编写递归函数了，在每一行，我们都不断的尝试一个坐标点，只要它和之前已有的结果都不冲突，那么就可以放入数组中作为下一次递归的开始值。

这样，如果递归函数顺利的来到了 rowIndex === n 的情况，说明之前的条件全部满足了，一个 n皇后 的解就产生了。

/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function (n) {
  let res = []

  // 已摆放皇后的列下标
  let columns = []
  // 已摆放的皇后的对角线1下标 左下 -〉右上
  // 计算某个坐标是否在这个对角线的方式是 [行下标 + 列下标] 是否相等
  let dia1 = []
  // 已摆放的皇后的对角线2下标 左上 -〉右下
  // 计算某个坐标是否在这个对角线的方式是 [行下标 - 列下标] 是否相等
  let dia2 = []

  // 尝试在一个n皇后问题中 摆放第index行内的皇后位置
  let putQueue = (rowIndex, row) => {
    if (rowIndex === n) {
      res.push(generateBoard(row))
      return
    }

    // 尝试摆放第index行的皇后 尝试[0, n-1]列
    for (let columnIndex = 0; columnIndex < n; columnIndex++) {
      // 在列上不冲突
      let columnNotConflict = !columns[columnIndex]
      // 在对角线1上不冲突
      let dia1NotConflict = !dia1[rowIndex + columnIndex]
      // 在对角线2上不冲突
      let dia2NotConflict = !dia2[rowIndex - columnIndex]

      if (columnNotConflict && dia1NotConflict && dia2NotConflict) {
        columns[columnIndex] = true
        dia1[rowIndex + columnIndex] = true
        dia2[rowIndex - columnIndex] = true

        putQueue(rowIndex + 1, row.concat(columnIndex))

        columns[columnIndex] = false
        dia1[rowIndex + columnIndex] = false
        dia2[rowIndex - columnIndex] = false
      }
    }
  }

  putQueue(0, [])

  return res
}

function generateBoard(row) {
  let n = row.length
  let res = []
  for (let y = 0; y < n; y++) {
    let cur = ''
    for (let x = 0; x < n; x++) {
      if (x === row[y]) {
        cur += 'Q'
      } else {
        cur += '.'
      }
    }
    res.push(cur)
  }
  return res
}

N 皇后 II-52

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

思路

• 每次尝试将皇后放置在当前行的每一列上，确保没有冲突（列、主对角线、副对角线）。
• 如果成功放置了 n 个皇后，增加解法计数。
• 剪枝：在每一步的放置中，跳过不合法的位置。

/**
 * @param {number} n
 * @return {number}
 */
var totalNQueens = function (n) {
  let count = 0

  function backtrack(row, cols, diagonals1, diagonals2) {
    if (row === n) {
      count++ // 成功放置n个皇后，计数加1
      return
    }

    for (let col = 0; col < n; col++) {
      const diag1 = row + col // 主对角线标识
      const diag2 = row - col + n // 副对角线标识

      // 检查是否冲突
      if (cols[col] || diagonals1[diag1] || diagonals2[diag2]) {
        continue // 冲突，跳过当前列
      }

      // 标记为已占用
      cols[col] = diagonals1[diag1] = diagonals2[diag2] = true

      // 递归尝试下一行
      backtrack(row + 1, cols, diagonals1, diagonals2)

      // 撤销标记（回溯）
      cols[col] = diagonals1[diag1] = diagonals2[diag2] = false
    }
  }

  // 初始化列和对角线的占用标记
  backtrack(
    0,
    Array(n).fill(false),
    Array(2 * n).fill(false),
    Array(2 * n).fill(false)
  )

  return count
}

解数独-37

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 '.' 表示。

一个数独。

答案被标成红色。

Note:

给定的数独序列只包含数字 1-9 和字符 '.' 。 你可以假设给定的数独只有唯一解。 给定数独永远是 9x9 形式的。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/sudoku-solver 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

又是一道 hard 难度的题，我感觉这题整体的思路不难找，但是要写很多代码，抽了几个函数以后代码量会少一点。

其实思路和 N 皇后问题类似，都是在每次递归求解下一项的时候（在这个问题里是求解下一个待填充的格子）需要保证以下几点：

• 当前行没有出现过这个数字。
• 当前列没有出现过这个数字。
• 当前所属的九宫格中没有出现过这个数字。

前置

首先对整个二维数组进行一次全面扫描，确立以下状态，用几个变量记录这些某个数字是否出现的状态：

• rows 一个二维数组长度为 9，记录每一行中某个数字的出现状态，比如 rows[0][1] 代表第 0 行中是否出现过数字 1。
• columns 一个二维数组长度为 9，记录每一列中某个数字的出现状态，比如 columns[0][1] 代表第 0 列中是否出现过数字 1。
• grids 一个二维数组长度为 3，记录每个九宫格中某个数字的出现状态，比如 grids[0][1] 代表第 0 个九宫格中是否出现过数字 1。

grids 的分布如图所示：

每个数字分别代表 x, y，比如 21 代表 grids 中的 grids[1][2]，并且这个 grids[1][2] 的值还是一个数组，这个数组的第 i 项就代表 i 这个数字是否在这个九宫格中出现过。比如 grids[1][2][5] 代表 5 这个数字是否在 12 这个九宫格中出现过。

再用 pending 数组用来记录在第一次扫描中遇到的值为.的格子的坐标，作为待处理的坐标集合。

解题

首先对二维数组做一次扫描，确立上述的状态变量。

然后定义一个 helper 递归函数，整个函数只需要接受一个参数 startPendingIndex 代表当前在处理的是第几个 pending 队列中的坐标 。

在每次递归的时候，都从 1 ~ 9 循环选取一个值，判断当前的值符合前面的三个条件，然后尝试选取该值并记录在 行、列、九宫格 中，递归进入下一个 pendingIndex，如果不满足条件的话，函数会回溯到当前位置，那么此时就把 行、列、九宫格 中记录的当前值的状态清空掉，继续循环。

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
let solveSudoku = function (board) {
  let rows = initTwoDimensionalArray(9)
  let columns = initTwoDimensionalArray(9)
  let grids = initTwoDimensionalArray(3)

  // 待处理下标队列 第一次扫描的时候记录下来
  let pending = []

  for (let y = 0; y < 9; y++) {
    for (let x = 0; x < 9; x++) {
      let cell = board[y][x]
      if (cell === '.') {
        // 待填充的数独格子 记录在队列中
        pending.push([x, y])
        continue
      }
      // 记录下当前下标
      recordCell(x, y, cell)
    }
  }

  let helper = (startPendingIndex) => {
    if (startPendingIndex === pending.length) {
      return true
    }

    let [x, y] = pending[startPendingIndex]

    for (let i = 1; i <= 9; i++) {
      let cur = i.toString()
      if (isValid(x, y, cur)) {
        board[y][x] = cur
        recordCell(x, y, cur)
        if (helper(startPendingIndex + 1)) {
          return true
        } else {
          board[y][x] = '.'
          restoreCell(x, y, cur)
        }
      }
    }
  }

  helper(0)

  function recordCell(x, y, cell) {
    rows[y][cell] = true
    columns[x][cell] = true
    let [gridX, gridY] = findGridIndex(x, y)
    if (!grids[gridY][gridX]) {
      grids[gridY][gridX] = new Map()
    }
    grids[gridY][gridX].set(cell, true)
  }

  function restoreCell(x, y, cell) {
    rows[y][cell] = false
    columns[x][cell] = false
    let [gridX, gridY] = findGridIndex(x, y)
    grids[gridY][gridX].set(cell, false)
  }

  function isValid(x, y, cell) {
    let isYConflict = rows[y][cell]
    let isXConflict = columns[x][cell]
    let [gridX, gridY] = findGridIndex(x, y)
    let grid = grids[gridY][gridX]
    let isGridConflict = grid && grid.get(cell)
    return !isYConflict && !isXConflict && !isGridConflict
  }
}

function initTwoDimensionalArray(length) {
  let ret = []
  for (let i = 0; i < length; i++) {
    ret.push([])
  }
  return ret
}

function findGridIndex(x, y) {
  return [Math.floor(x / 3), Math.floor(y / 3)]
}

动态规划：将原问题拆解成若干子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案。本质还是递归问题，用于解决 重叠子问题 + 最优子结构，自底向上的解决问题。也可以使用记忆化搜索，自顶向下的解决问题。

爬楼梯-70

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2 输出： 2 解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入： 3 输出： 3 解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/climbing-stairs 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题的思路是，对于到达任意一个阶梯 n，都可以分为「从前两个台阶跨两步到达」和「从前一个台阶跨一步到达」，而本题的目的是取「方式之和」，所以动态规划的状态转移方程是 dp[n] = dp[n - 1] + dp[n - 2]

1. 从上一阶的位置跨一步，取 dp[i - 1]的到达方式数量。
2. 从上两阶的位置跨两步，取 dp[i - 2]的到达方式数量。

然后把这两个方式的数量相加，就是到达第 n 阶的方式总数。

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function (n) {
  let dp = []

  dp[1] = 1
  dp[2] = 2

  for (let i = 3; i <= n; i++) {
    // 到达第 n 阶的方式
    // 1.从上一阶的位置跨一步 取dp[i-1]的到达方式数量
    // 1.从上两阶的位置跨两步 取dp[i-2]的到达方式数量
    // 把两种的方式数量相加，即可得到到达第 n 阶方式数量
    dp[i] = dp[i - 2] + dp[i - 1]
  }

  return dp[n]
}

三角形最小路径和-120

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/triangle 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

1. 状态定义

   • 用 dp[i][j] 表示到达位置 (i, j) 的最小路径和。

2. 递推公式

   从底向上递推：

   dp[i][j] = triangle[i][j] + min(dp[i + 1][j], dp[i + 1][j + 1])

3. 优化空间复杂度

   • 由于每次计算只依赖下一行数据，可以将二维数组压缩成一维数组 dp，只保留当前行和下一行的状态。

/**
 * @param {number[][]} triangle
 * @return {number}
 */
var minimumTotal = function (triangle) {
  const n = triangle.length
  // 初始化 dp 为最后一行
  let dp = [...triangle[n - 1]]

  // 从倒数第二行开始递推
  for (let i = n - 2; i >= 0; i--) {
    for (let j = 0; j <= i; j++) {
      dp[j] = triangle[i][j] + Math.min(dp[j], dp[j + 1])
    }
  }

  // 返回 dp[0] 即顶点的最小路径和
  return dp[0]
}

最小路径和-64

给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

示例 1：

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

链接

思路

1. 状态定义:

   • 用 dp[i][j] 表示从起点 (0, 0) 到位置 (i, j) 的最小路径和。

2. 递推公式:

   • 如果在第一行或第一列：

     dp[i][j] = grid[i][j] + 左边或上边的路径和

   • 一般位置：

     dp[i][j]=grid[i][j]+min(dp[i−1][j],dp[i][j−1])

3. 初始化:

   • 第一行和第一列只能从一个方向到达，因此需要单独处理。

4. 优化空间复杂度:

   • 使用一维数组保存状态，每次只保留上一行的结果，从而将空间复杂度优化到 O(n)。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
  const m = grid.length
  const n = grid[0].length

  // 使用一维数组保存状态
  const dp = Array(n).fill(0)

  // 初始化第一行
  dp[0] = grid[0][0]
  for (let j = 1; j < n; j++) {
    dp[j] = dp[j - 1] + grid[0][j]
  }

  // 填充dp数组
  for (let i = 1; i < m; i++) {
    dp[0] += grid[i][0] // 更新第一列
    for (let j = 1; j < n; j++) {
      dp[j] = grid[i][j] + Math.min(dp[j], dp[j - 1])
    }
  }

  // 返回最后一个位置的最小路径和
  return dp[n - 1]
}

整数拆分-343

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。 示例 2:

输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。 说明: 你可以假设 n 不小于 2 且不大于 58。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/integer-break 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题在求解每个子问题 i 的时候，都需要另外循环一个 j，这个 j 从 1 开始把 i 拆分成 i - j。

比如 3 需要拆分成 1,2 和 2,1，4需要拆分成 1,3、2,2、3,1。

以求 max(3) 的时候为例：

1. 先考虑 1 * max(2)、 2 * max(1)
2. 还需要考虑 1 * 2、2 * 1 也就是把右侧直接作为一个值相乘，而不是拿它拆分后的最大乘积（不然这里只能求出 1 * dp[2]，也就是 1 * 1 * 1 = 1，其实是小于 1 * 2 = 2 的）。

也就是说，状态转移方程是： dp[i] = max(j * (i - j), j * dp[i - j])。

/**
 * @param {number} n
 * @return {number}
 */
var integerBreak = function (n) {
  const dp = Array(n + 1).fill(0)
  dp[1] = 1

  for (let i = 2; i <= n; i++) {
    for (let j = 1; j < i; j++) {
      dp[i] = Math.max(dp[i], j * (i - j), j * dp[i - j])
    }
  }

  return dp[n]
}

解码方法-91

一条包含字母 A-Z 的消息通过以下方式进行了编码：

'A' -> 1 'B' -> 2 ... 'Z' -> 26 给定一个只包含数字的非空字符串，请计算解码方法的总数。

示例 1:

输入: "12"
输出: 2
解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。
示例 2:

输入: "226"
输出: 3
解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/decode-ways
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

很坑的一道题，从后往前确定每个字符串下标位置开头会有几种答案，状态转移方程是：

dp[i] = tryOneChar + tryTwoChar

注意：

1. 如果当前位置只选一个字符，如果这个字符是 0，那么不管后面有几种解，这个位置只选一个字符的解都是 0 个。
2. 如果当前位置选两个字符，如果字符的开头是 0 或者字符整体是 00，都视为 0 个解。
3. 注意处理倒数第二个字符时，dp[i + 2] 溢出。

其他没什么了。

/**
 * @param {string} s
 * @return {number}
 */
var numDecodings = function (s) {
  let dp = []
  let n = s.length
  if (!n) {
    return 0
  }

  dp[n - 1] = isZeroStr(s[n - 1]) ? 0 : 1
  for (let i = n - 2; i >= 0; i--) {
    let tryOneChar = 0
    let curChar = s[i]
    if (!isZeroStr(curChar)) {
      tryOneChar = dp[i + 1] === 0 ? 0 : 1 * dp[i + 1]
    }

    let tryTwoChar = 0
    let twoChar = s[i] + s[i + 1]
    if (!isZeroStr(twoChar) && !isZeroStr(curChar) && Number(twoChar) <= 26) {
      tryTwoChar = dp[i + 2] === 0 ? 0 : dp[i + 2] ? dp[i + 2] * 1 : 1
    }
    dp[i] = tryOneChar + tryTwoChar
  }

  return dp[0]
}

function isZeroStr(str) {
  return Number(str) === 0
}

打家劫舍 - 198

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
  偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
  偷窃到的最高金额 = 2 + 9 + 1 = 12 。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/house-robber 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

动态规划的一个很重要的过程就是找到「状态」和「状态转移方程」，在这个问题里，设 i 是当前屋子的下标，状态就是 以 i 为起点偷窃的最大价值

在某一个房子面前，盗贼只有两种选择：偷或者不偷。

1. 偷的话，价值就是「当前房子的价值」+「下两个房子开始盗窃的最大价值」
2. 不偷的话，价值就是「下一个房子开始盗窃的最大价值」

在这两个值中，选择最大值记录在 dp[i]中，就得到了以 i 为起点所能偷窃的最大价值。。

动态规划的起手式，找基础状态，在这题中，以终点为起点的最大价值一定是最好找的，因为终点不可能再继续往后偷窃了，所以设 n 为房子的总数量， dp[n - 1] 就是 nums[n - 1]，小偷只能选择偷窃这个房子，而不能跳过去选择下一个不存在的房子。

那么就找到了动态规划的状态转移方程：

// 抢劫当前房子
robNow = nums[i] + dp[i + 2] // 「当前房子的价值」 + 「i + 2 下标房子为起点的最大价值」

// 不抢当前房子，抢下一个房子
robNext = dp[i + 1] //「i + 1 下标房子为起点的最大价值」

// 两者选择最大值
dp[i] = Math.max(robNow, robNext)

，并且从后往前求解。

/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function (nums) {
  if (!nums.length) {
    return 0
  }
  let dp = []

  for (let i = nums.length - 1; i >= 0; i--) {
    let robNow = nums[i] + (dp[i + 2] || 0)
    let robNext = dp[i + 1] || 0

    dp[i] = Math.max(robNow, robNext)
  }

  return dp[0]
}

打家劫舍 II-213

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

示例 1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 3：

输入：nums = [1,2,3]
输出：3

链接

思路

1. 问题拆分：

   • 如果第一个房屋被偷，那么最后一个房屋不能被偷。
   • 如果第一个房屋不被偷，那么最后一个房屋可以被偷。
   • 因此，可以将问题拆分为两个子问题：
     1. 计算从第 1 个房屋到倒数第 2 个房屋的最大金额。
     2. 计算从第 2 个房屋到最后一个房屋的最大金额。

2. 子问题求解：

   • 子问题是一个简单的线性动态规划问题：

     • 定义 dp[i]dp[i]dp[i] 为从第 1 个房屋到第 iii 个房屋可以偷窃的最大金额。

     • 状态转移方程为：

       dp[i]=max(dp[i−1],dp[i−2]+nums[i])

     • 初始化：

       ;(dp[0] = nums[0]), (dp[1] = max(nums[0], nums[1]))

3. 取两种情况的最大值：

   • 最大金额为：

     max_amount=max(rob(0,n−2),rob(1,n−1))

/**
 * @param {number[]} nums
 * @return {number}
 */
function rob(nums) {
  const n = nums.length
  if (n === 1) return nums[0]

  // 子问题：线性打家劫舍
  function robRange(start, end) {
    let prev2 = 0,
      prev1 = 0

    for (let i = start; i <= end; i++) {
      const curr = Math.max(prev1, prev2 + nums[i])
      prev2 = prev1
      prev1 = curr
    }

    return prev1
  }

  // 考虑两种情况：不偷最后一个房子 或 不偷第一个房子
  return Math.max(robRange(0, n - 2), robRange(1, n - 1))
}

打家劫舍 |||-337

在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。

计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

示例 1:

输入: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \
     3   1

输出: 7 解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7. 示例 2:

输入: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \
 1   3   1

输出: 9 解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/house-robber-iii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题的题目上存在误导，并不是简单的跳一级去找最大值就可以，注意考虑这种情况：

     2
    / \
   1   3
  / \
 n  4

这种情况下并不要跳级，而是第二层的 3 和第三层的 4 是去凑成打劫的最优解。

所以此题的解法是从顶层节点开始

1. 抢劫当前的节点，那么儿子层就没法抢劫了，只能抢劫孙子层。
2. 不抢劫当前节点，那么可以抢劫儿子层。

这两者对比求出的最大值，就是最优结果。

自顶向下记忆化

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
let memo = new WeakMap()
var rob = function (root) {
  if (!root) {
    return 0
  }

  let memorized = memo.get(root)
  if (memorized) {
    return memorized
  }

  let notRob = rob(root.left) + rob(root.right)
  let robNow =
    (root.val || 0) +
    (root.left ? rob(root.left.left) + rob(root.left.right) : 0) +
    (root.right ? rob(root.right.left) + rob(root.right.right) : 0)

  let max = Math.max(notRob, robNow)
  memo.set(root, max)
  return max
}

自底向上动态规划

上面的解法是自顶向下的，那么动态规划的自底向上解法应该怎么做呢？我们上一层的打劫最优解是依赖下一层的，所以显然我们应该先从最下层的求解。思考提取关键字「层序」、「自底向上」。

灵机一动，用递归回溯法配合BFS：

递归版的 BFS 先求出当前队列里所有的子节点，放入一个新的队列 subs 中，然后进一步 BFS 这个子节点队列 subs。

那么这个递归 subs 之后的一行，就代表递归后回溯的时机，我们把「动态规划」求解的部分放在递归函数的后面， 当 BFS 到达了最后一层后，发现没有节点可以继续 BFS 了，这个时候最底层的函数调用慢慢弹出栈，从最底层慢慢往上回溯，

那么 「动态规划」求解的部分就是「自底向上」的了，我们在上层中求最优解的时候，一定能取到下面层的最优解。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var rob = function (root) {
  if (!root) return 0
  let dp = new Map()
  dp.set(null, 0)

  let bfs = (nodes) => {
    if (!nodes.length) {
      return
    }

    let subs = []
    for (let node of nodes) {
      if (node.left) {
        subs.push(node.left)
      }
      if (node.right) {
        subs.push(node.right)
      }
    }

    bfs(subs)

    // 到达最底层后，最底层先开始dp
    // 再一层层回溯
    for (let node of nodes) {
      // 打劫这个节点
      let robNow = node.val
      if (node.left) {
        robNow += dp.get(node.left.left)
        robNow += dp.get(node.left.right)
      }
      if (node.right) {
        robNow += dp.get(node.right.left)
        robNow += dp.get(node.right.right)
      }

      // 不打劫这个节点，打劫下一层
      let robNext = dp.get(node.left) + dp.get(node.right)
      dp.set(node, Math.max(robNow, robNext))
    }
  }

  bfs([root])

  return dp.get(root)
}

买卖股票的最佳时机含冷冻期-309

给定一个整数数组prices，其中第 prices[i] 表示第 *i* 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

• 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

**注意：**你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

示例 2:

输入: prices = [1]
输出: 0

链接

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function (prices) {
  const n = prices.length
  if (n === 0) return 0

  // 初始化
  let hold = -prices[0] // dp[i][0] 持有股票
  let freeze = 0 // dp[i][1] 冷冻期
  let noFreeze = 0 // dp[i][2] 非冷冻期

  for (let i = 1; i < n; i++) {
    const preHold = hold
    const prevFreeze = freeze

    // 更新状态
    hold = Math.max(hold, noFreeze - prices[i])
    freeze = preHold + prices[i]
    noFreeze = Math.max(noFreeze, prevFreeze)
  }

  // 返回最大值
  return Math.max(freeze, noFreeze)
}

背包（01背包

给定一个数组 w 代表物品的重量，v 数组代表物品的价值，C 代表背包的总容量。求背包最多能装下价值多少的物品。每个物品只能装一次。

物品的重量是 [1, 2, 3]，物品的价值是 [6, 10, 12]，背包重量是 5。

这种情况下最优解是 22。

递归版

思路

这题递归的思路就是对于以每一个物品为起点，分为两种情况。装当前物品和不装当前物品，求它们之间最大值作为结果。

1. 选择装，最大值 = 当前物品的价值 + 递归去找减去当前物品重量后的可以装的最大价值。 v[i] + best(i - 1, c - w[i])
2. 选择不装，最大值 = 背包重量不变，递归去找以上一件物品为起点可以装的最大价值。（在这个流程里又可会继续发展出装与不装的选择） best(i - 1, c)

/**
 *
 * @param {number[]} w 物品的重量集合
 * @param {number[]} v 物品的价值集合
 * @param {number} C 背包容量
 */
function knapsack01(w, v, C) {
  let n = w.length - 1

  return bestValue(w, v, n, C)
}

// 用 [0...index] 的物品
// 填充容积为c的背包的最大价值
function bestValue(w, v, index, c) {
  if (index < 0 || c <= 0) return 0

  let max = bestValue(w, v, index - 1, c)

  // 装背包之前需要先判断这个当前背包还可以容纳下这个物品
  if (c >= w[index]) {
    max = Math.max(
      // 不装进背包
      max,
      // 装进背包
      v[index] + bestValue(w, v, index - 1, c - w[index])
    )
  }

  return max
}

动态规划版

这是 DP 问题的例题中第一个出现二维 dp 数组的问题，因此标为例题详解。

在这个问题中，子问题可以从递归版中总结出来，就是「装进背包」 or 「不装进背包」的选择。二维数组大致是这个结构：

      1  2  3  4  5  <- 这一层代表背包的容量
物品1
物品2
物品3

↑ 这一层代表可选的物品。

注意可选物品也就是纵轴，它下面的层级是上面层级最优解的叠加值，也就是物品3的层级是包含了可以选择物品2和物品1的情况下的最大价值的。

所以这题的子问题就是可选物品由少增多的情况下，不断求解每个背包容量情况下的最优解。当双层循环遍历完毕后，最右下角的值也就代表了「包含了所有物品的情况下，并且容量为C时」的最优解。

/**
 *
 * @param {number[]} w 物品的重量集合
 * @param {number[]} v 物品的价值集合
 * @param {number} C 背包容量
 */
let knapsack01 = function (w, v, C) {
  let n = w.length
  if (n === 0) return 0

  // 构建二维数组dp表
  // x轴代表背包容量 y轴代表考虑的物品情况
  // 第一行只考虑一种物品（基准情况）
  // 第二行考虑一和二两种（通过拿取二和不拿二，再去组合第一行的最佳情况来求最大值）
  // 第三行以此类推
  let memo = new Array(n)
  for (let i = 0; i < memo.length; i++) {
    memo[i] = new Array(C + 1).fill(0)
  }

  // 基础情况 背包在各个容量的情况下 只考虑第一个物品时的最优解
  for (let j = 0; j <= C; j++) {
    memo[0][j] = j >= w[0] ? v[0] : 0
  }

  for (let i = 1; i < n; i++) {
    for (let j = 0; j <= C; j++) {
      let weight = w[i]
      let restWeight = j - weight
      // 有足够容量的情况下 选择当前的的物品 并且用剩余的重量去找前面几个物品组合的最优解
      let pickNow = j >= weight ? v[i] + memo[i - 1][restWeight] : 0

      // 另一种选择 这个物品不放进背包了 直接求用这个背包容量组合前面几种物品的最优解
      let pickPrev = memo[i - 1][j]

      memo[i][j] = Math.max(pickNow, pickPrev)
    }
  }

  return memo[n - 1][C]
}

console.log(knapsack01([1, 2, 3], [6, 10, 12], 5))

优化 1

由于纵轴的每一层的最优解都只需要参考上一层节点的最优解，因此可以只保留两行。通过判断除 2 取余来决定“上一行”的位置。此时空间复杂度是 O(2n)

优化 2

由于每次参考值都只需要取上一行和当前位置左边位置的值（因为剩余重量的最优解一定在左边），因此可以把问题转为从右向左求解，并且在求解的过程中不断覆盖当前列的值，而不会影响下一次求解。此时空间复杂度是 O(n)。

并且在这种情况下对于时间复杂度也可以做优化，由于背包所装的容量，也就是 j，它是倒序遍历的，那么当发现它小于当前物品的重量时，说明不可能装下当前物品了，此时直接结束本层循环即可，因为左边的值一定是「不选当前物品时的最大价值」，也就是在上一轮循环中已经求得的值。

最长上升子序列-300

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。 你算法的时间复杂度应该为 O(n2) 。 进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?

leetcode-cn.com/problems/longest-increasing-subsequence

思路

从前往后求解，对于每个值 i，都需要从 j = 0 ~ i 依次求解。

只要 i > j，就说明 [j, i] 可以形成一个上升子序列，那么只需要把已经求解好的 j 位置的最长上升序列的长度 dp[j] 拿出来 +1 即可得到 i 位置的最长上升序列长度。从 0 ~ j 循环找出其中和 i 形成的序列长度的最大值，记录在 dp[i] 位置即可。

最后从 dp 数组中取出最大值，就是这个问题的解。

/**
 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function (nums) {
  let dp = []
  let n = nums.length
  if (!n) {
    return 0
  }

  dp[0] = 1
  for (let i = 1; i < n; i++) {
    let num = nums[i]
    let max = 1
    // j 从 [0,i] 依次求出可以和 i 组成的最长上升子序列
    for (let j = 0; j < i; j++) {
      let preNum = nums[j]
      if (num > preNum) {
        // 循环中不断更新max值
        max = Math.max(max, dp[j] + 1)
      }
    }
    dp[i] = max
  }

  return Math.max(...dp)
}

摆动序列-376

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例 1:

输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。
示例 2:

输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。
示例 3:

输入: [1,2,3,4,5,6,7,8,9]
输出: 2
进阶:
你能否用 O(n) 时间复杂度完成此题?

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/wiggle-subsequence 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

摆动序列，dp 中对于每一个值的求解都需要记录 less 和 more，当前值的最长子序列的最后一个方向是上升，那么就记录为 less，反之记录为 more。

在后续的求解中，如果当前的数字大于前面的数字，那么就去找前面的 more 最优解，并且记录在本轮 dp 中的 less 属性上。反之记录在 more 属性上。

最后找出所有 less、more 中的最大值即可。

/**
 * @param {number[]} nums
 * @return {number}
 */
var wiggleMaxLength = function (nums) {
  let dp = []
  let n = nums.length
  if (!n) {
    return 0
  }

  dp[0] = {
    less: 1,
    more: 1
  }

  let res = 1

  for (let i = 1; i < n; i++) {
    let num = nums[i]
    dp[i] = {
      less: 1,
      more: 1
    }
    for (let j = 0; j < i; j++) {
      let prevNum = nums[j]
      let max = 1
      if (num > prevNum) {
        dp[i].less = Math.max(dp[i].less, dp[j].more + 1)
      } else if (num < prevNum) {
        dp[i].more = Math.max(dp[i].more, dp[j].less + 1)
      }
    }
    res = Math.max(res, dp[i].more, dp[i].less)
  }
  return res
}

最长公共子序列-1143

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace"，它的长度为 3。
示例 2:

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。
示例 3:

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。


提示:

1 <= text1.length <= 1000
1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/longest-common-subsequence 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

把两个字符长度都置为 1 开始规划基础状态，注意这是一个二维的 dp 数组, dp[m][n] 中的 m 和 n 分别代表字符串 1 的长度和字符串 2 的长度，这个坐标的状态就是「字符串 1 长度为 m 且字符串 2 长度为 n 时的最长公共序列长度」。

对于 dp[m][n] 来说，分为两种情况：

1. s1[m] === s2[n] 字符相等，那么就直接等于 1 + dp[m - 1][n - 1]，也就是当前相等所得到的长度 1 加上两个字符各减去一位后的最长子序列长度。
2. s1[m] !== s2[n] 字符不相等，那么就分别尝试把两边各减去一位，求它们的最长子序列长度中的 最大值，也就是 max(dp[m][n - 1], dp[m - 1][n])。

理清楚这个关系后，就可以开始写传统的二维数组 dp 求解了，动态规划是自底向上的，所以我们从字符位置都在 0 的情况开始，慢慢的向上求解。

注意这题里要提前把溢出情况比如 dp[-1][0]、dp[-1][-1] 提前设置为 0，防止访问时报错。比如在求解 dp[0][0] 并且两个字符串的第 0 位都相同的时候就会转而去求 dp[-1][-1]

/**
 * @param {string} text1
 * @param {string} text2
 * @return {number}
 */
var longestCommonSubsequence = function (text1, text2) {
  let n1 = text1.length
  let n2 = text2.length

  let dp = []

  for (let i1 = 0; i1 <= n1; i1++) {
    dp[i1] = []
    dp[i1][0] = 0
  }
  dp[0] = Array(n2 + 1).fill(0)

  for (let i1 = 1; i1 <= n1; i1++) {
    for (let i2 = 1; i2 <= n2; i2++) {
      let str1 = text1[i1 - 1]
      let str2 = text2[i2 - 1]

      if (str1 === str2) {
        dp[i1][i2] = 1 + dp[i1 - 1][i2 - 1]
      } else {
        dp[i1][i2] = Math.max(dp[i1 - 1][i2], dp[i1][i2 - 1])
      }
    }
  }

  return dp[n1][n2]
}

分割等和子集（01背包的变种）-416

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

每个数组中的元素不会超过 100 数组的大小不会超过 200 示例 1:

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

输入: [1, 2, 3, 5]

输出: false

解释: 数组不能分割成两个元素和相等的子集.

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/partition-equal-subset-sum 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题的难点在于如何转化为 01 背包问题，要想清楚如果数组可以分割成两个相等的数组，那么我们的目标其实是求有没有子数组的和为「整个数组的和的一半」（下文称为 target）。而由于这个和是「整个数组」的值加起来的一半求得的，所以其中的一半我们找到了，此时另外的子数组相加的值一定也是一半，也就是 target。

只要想清楚这个问题，题目就迎刃而解了。

这里的二维 DP 表：

纵坐标 i 代表数组中覆盖到的元素，从第一个元素开始（ i = 2 是包含了 i = 1 和 i = 0 的情况的。）。

横坐标 j 代表 [0...target] 中的值 j 是否可以由 i 覆盖到的数值凑得，它是 true 或 false。

每一步也分为「拿当前的元素」和「不拿当前的元素」。

1. 拿的话，结果就变为 dp[i - 1]j - nums[i]] （看看用前几个数能不能凑成「目标值 - 当前的值」）。
2. 不拿的话，结果就变为 dp[i - 1][j] （不用这个数，前几个数能不能凑成当前的值）
3. 特殊情况，当前的值可以直接凑成目标值，也算 true。

只要这三项中有任意一项为 true，那么结果就为 true。

另外有几个注意点：

1. 一开始就可以判断，数组之和除以二后不是整数的话，直接失败。因为这一定不可能是两个整数子数组相凑的结果。
2. 只要用任意数量的子数组可以拼凑出来 target 的值，也就是 dp 数组的任意一层的最右边的值计算出是 true，那么整题的结果就为 true。因为不论你用几个值凑出了 target 值，哪怕只用了一个值。另外剩下的值之和一定也是 target。

说实话这篇题解讲的更好：

leetcode-cn.com/problems/partition-equal-subset-sum/solution/0-1-bei-bao-wen-ti-xiang-jie-zhen-dui-ben-ti-de-yo

/**
 * @param {number[]} nums
 * @return {boolean}
 */
let canPartition = function (nums) {
  let n = nums.length

  let sum = nums.reduce((a, b) => a + b)

  let target = sum / 2

  // 数据不是整数 直接return
  if (Math.ceil(target) !== target) {
    return false
  }

  let dp = new Array(n)
  for (let i = 0; i < dp.length; i++) {
    dp[i] = new Array(target + 1).fill(false)
  }

  // 列代表可以选择去凑数的数值
  for (let i = 0; i < dp.length; i++) {
    // 行代表是否可以凑到这个数字j
    for (let j = 0; j <= target; j++) {
      // 不用当前数，直接选择前一行的结果
      let pickPrev = (dp[i - 1] ? dp[i - 1][j] : false) || false

      // 拿出当前数，并且从前一行里找其他的值能否凑成剩下的值
      let pickCurrentAndPrev =
        (dp[i - 1] ? dp[i - 1][j - nums[i]] : false) || false

      // 只拿的值直接去凑目标值
      let pickCurrent = j === nums[i]

      // 任意一者满足 即可理解成 「i下标的值」配合「i下标之前的数值」 可以一起凑成目标值
      let can = pickPrev || pickCurrent || pickCurrentAndPrev

      dp[i][j] = can

      // 只要任意一行的 target 列满足条件 即可认为有「子数组」可以凑成目标值 直接返回 true
      if (j === target && can) {
        return true
      }
    }
  }
  return dp[n - 1][target]
}

零钱兑换-322

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

[链接/]https://leetcode.cn/problems/coin-change()

思路

1. 定义状态：

   • 用 dp[j 表示凑成金额 j 所需的最少硬币数量。

2. 状态转移方程：

   对于每种硬币 coin，若金额 j 能被当前硬币 coin 凑成

   • 不选当前硬币的情况 dp[j]，或者
   • 选当前硬币的情况 dp[j−coin]+1。

3. 初始化：

   • dp[0]=0，即凑成金额 0 不需要任何硬币。
   • 其他值初始化为一个较大的数（如 amount+1），表示暂时无法凑成。

4. 最终结果：

   • 若 dp[amount]>amount，说明无法凑成该金额，返回 -1；
   • 否则返回 dp[amount]。

/**
 * @param {number[]} coins
 * @param {number} amount
 * @return {number}
 */
var coinChange = (coins, amount) => {
  const dp = Array(amount + 1).fill(amount + 1)

  // 初始化
  dp[0] = 0

  // 动态规划
  for (const coin of coins) {
    for (let j = coin; j <= amount; j++) {
      dp[j] = Math.min(dp[j], dp[j - coin] + 1)
    }
  }

  // 检查是否有解
  return dp[amount] > amount ? -1 : dp[amount]
}

一和零-474

在计算机界中，我们总是追求用有限的资源获取最大的收益。

现在，假设你分别支配着 m 个 0 和 n 个 1。另外，还有一个仅包含 0 和 1 字符串的数组。

你的任务是使用给定的 m 个 0 和 n 个 1 ，找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。

注意:

给定 0 和 1 的数量都不会超过 100。 给定字符串数组的长度不会超过 600。

示例 1:

输入: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
输出: 4

解释: 总共 4 个字符串可以通过 5 个 0 和 3 个 1 拼出，即 "10","0001","1","0" 。
示例 2:

输入: Array = {"10", "0", "1"}, m = 1, n = 1
输出: 2

解释: 你可以拼出 "10"，但之后就没有剩余数字了。更好的选择是拼出 "0" 和 "1" 。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/ones-and-zeroes 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

直接转载 liweiwei大佬的题解 吧，讲的很好了。

思路：把总共的 0 和 1 的个数视为背包的容量，每一个字符串视为装进背包的物品。这道题就可以使用 0-1 背包问题的思路完成。这里的目标值是能放进背包的字符串的数量。

思路依然是“一个一个尝试，容量一点一点尝试”，每个物品分类讨论：选与不选。

第 1 步：定义状态

依然是尝试「题目问啥，就把啥定义成状态」。 dp[i][j][s] 表示输入字符串在子区间 [0, s] 能够使用 i 个 0 和 j 个 1 的字符串的最大数量。

第 2 步：状态转移方程

dp[i][j][k]= max(
  // 不选择当前字符串
  dp[i][j][k - 1],
  // 选择了当前字符串，用减掉可用个数后并且不能选择当前字符时的最优解
  dp[i - 当前字符使用 0 的个数][j - 当前字符使用 1 的个数][k - 1]
)

第 3 步：输出

输出是最后一个状态，即：dp[m][n][strs.length - 1]。

作者：liweiwei1419 链接：leetcode-cn.com/problems/ones-and-zeroes/solution/dong-tai-gui-hua-zhuan-huan-wei-0-1-bei-bao-wen-ti 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

/**
 * @param {string[]} strs
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
let findMaxForm = function (strs, m, n) {
  let sl = strs.length
  if (!sl) {
    return 0
  }

  let dp = []

  for (let i = 0; i <= m; i++) {
    dp[i] = []
    for (let j = 0; j <= n; j++) {
      dp[i][j] = []
      for (let s = 0; s < sl; s++) {
        let str = strs[s]
        let [strM, strN] = countMAndN(str)

        let pickOnlyPrev = dp[i][j][s - 1] || 0
        let pickCurAndPrev = 0
        if (i >= strM && j >= strN) {
          pickCurAndPrev = 1 + (dp[i - strM][j - strN][s - 1] || 0)
        }

        dp[i][j][s] = Math.max(pickCurAndPrev, pickOnlyPrev)
      }
    }
  }
  return dp[m][n][sl - 1]
}

function countMAndN(str) {
  let m = 0
  let n = 0
  for (let i = 0; i < str.length; i++) {
    if (str[i] === "0") {
      m++
    } else {
      n++
    }
  }
  return [m, n]
}

单词拆分-139

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。 你可以假设字典中没有重复的单词。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
     注意你可以重复使用字典中的单词。
示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/word-break 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

参考：leetcode-cn.com/problems/word-break/solution/shou-hui-tu-jie-san-chong-fang-fa-dfs-bfs-dong-tai

这题的动态规划思路不是很好想，

求 s 字符串是否可以由 wordDict 分割，可以转化为从 i = 0 ~ s.length 这个长度为 i 的字符串是否可以由它分割。

而每次对 dp[i] 的求解，可以再定一个变量 j，这个j 从 i ~ 0 遍历，分别把字符串分割为 j ~ i 和 0 ~ j 两部分，

只要：

1. dp[j] 为 true ，说明前 j 个字符已经在动态规划表中确定为可以由 wordDict 分割。
2. j ~ i 这串字符串在 wordDict 中出现，那么结合上一个条件，说明这一整串 0 ~ i 的字符都可以由 wordDict 分割。

那么 dp[i] 的结果也可以确定为 true。

/**
 * @param {string} s
 * @param {string[]} wordDict
 * @return {boolean}
 */
let wordBreak = function (s, wordDict) {
  let n = s.length
  if (!n) return true

  let wordSet = new Set(wordDict)
  let dp = []
  dp[0] = true

  for (let i = 0; i <= n; i++) {
    for (let j = i; j >= 0; j--) {
      let word = s.slice(j, i)
      if (wordSet.has(word) && dp[j]) {
        dp[i] = true
        break
      }
    }
  }

  return !!dp[n]
}

目标和-494

给定一个非负整数数组，a1, a2, ..., an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例：

输入：nums: [1, 1, 1, 1, 1], S: 3
输出：5
解释：

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

提示：

• 数组非空，且长度不会超过 20 。
• 初始的数组的和不会超过 1000 。
• 保证返回的最终结果能被 32 位整数存下。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/target-sum 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题的 DP 思路相对难找一点：

横坐标

首先需要确认的一点是，给定的 nums 数组的全部数字的和：

• 最小值 min 是全部选择负数形态的情况。
• 最大值 max 是全部选择正数形态的情况。

那么我们的这我们就遍历这两个值的区间，s = min ~ max 作为 DP 二维数组的横坐标。

纵坐标

纵坐标就按照背包问题的思路，从 n = 0 ~ nums.length 分别考虑选择n 个数字的情况下能去凑成横坐标的解的个数。

状态转移方程

每个数字 num 能够选择整数或负数，以 s = 2 这个坐标为例，假如我们之前已经规划过 [1, 1]，现在到了 [1, 1, 1] 的情况，当前拿到了一个新的数字 1 去凑 2：

• 选用正数的情况下就变成了用之前选择的几个数字去凑 2 - 1。
• 选用负数的情况下就变成了用之前选择的几个数字去凑 2 - (-1) 也就是 2 + 1。

所以状态转移方程是：

dp[n][s] = dp[n - 1][s - num] + dp[n - 1][s + num]

/**
 * @param {number[]} nums
 * @param {number} S
 * @return {number}
 */
let findTargetSumWays = function (nums, S) {
  let ns = nums.length
  if (!ns) {
    return 0
  }
  let min = nums.reduce((sum, cur) => sum - cur, 0)
  let max = nums.reduce((sum, cur) => sum + cur, 0)

  let dp = []
  for (let n = 0; n < ns; n++) {
    dp[n] = []
  }

  // 基础状态
  for (let s = min; s <= max; s++) {
    let num = nums[0]
    let pickPositive = s === num ? 1 : 0
    // 选负数形态
    let pickNegative = -s === num ? 1 : 0
    dp[0][s] = pickPositive + pickNegative
  }

  for (let n = 1; n < ns; n++) {
    for (let s = min; s <= max; s++) {
      let num = nums[n]
      // 选正数形态
      let pickPositive = dp[n - 1][s - num] || 0
      // 选负数形态
      let pickNegative = dp[n - 1][s + num] || 0
      dp[n][s] = pickNegative + pickPositive
    }
  }
  return dp[ns - 1][S] || 0
}

分发饼干-455

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i ，都有一个胃口值 gi ，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j ，都有一个尺寸 sj 。如果 sj >= gi ，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

注意：

你可以假设胃口值为正。 一个小朋友最多只能拥有一块饼干。

示例 1:

输入: [1,2,3], [1,1]

输出: 1

解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:

输入: [1,2], [1,2,3]

输出: 2

解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/assign-cookies 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

把饼干和孩子的需求都排序好，然后从最小的饼干分配给需求最小的孩子开始，不断的尝试新的饼干和新的孩子，这样能保证每个分给孩子的饼干都恰到好处的不浪费，又满足需求。

利用双指针不断的更新 i 孩子的需求下标和 j饼干的值，直到两者有其一达到了终点位置：

1. 如果当前的饼干不满足孩子的胃口，那么把 j++ 寻找下一个饼干，不用担心这个饼干被浪费，因为这个饼干更不可能满足下一个孩子（胃口更大）。
2. 如果满足，那么 i++; j++; count++ 记录当前的成功数量，继续寻找下一个孩子和下一个饼干。

/**
 * @param {number[]} g
 * @param {number[]} s
 * @return {number}
 */
var findContentChildren = function (g, s) {
  g.sort((a, b) => a - b)
  s.sort((a, b) => a - b)

  let i = 0
  let j = 0

  let count = 0
  while (j < s.length && i < g.length) {
    let need = g[i]
    let cookie = s[j]

    if (cookie >= need) {
      count++
      i++
      j++
    } else {
      j++
    }
  }

  return count
}

判断子序列-392

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

你可以认为 s 和 t 中仅包含英文小写字母。字符串 t 可能会很长（长度 ~= 500,000），而 s 是个短字符串（长度 <=100）。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

示例 1:
s = "abc", t = "ahbgdc"

返回 true.

示例 2:
s = "axc", t = "ahbgdc"

返回 false.

后续挑战 :

如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10 亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

致谢:

特别感谢 @pbrother](https://github.com/pbrother) 添加此问题并且创建所有测试用例。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/is-subsequence 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

判断字符串 s 是否是字符串 t 的子序列，我们可以建立一个 i 指针指向「当前 s 已经在 t 中成功匹配的字符下标后一位」。之后开始遍历 t 字符串，每当在 t 中发现 i 指针指向的目标字符时，就可以把 i 往后前进一位。

• 一旦i === t.length ，就代表 t 中的字符串全部按顺序在 s 中找到了，返回 true。
• 当遍历 s 结束后，就返回 false，因为 i 此时并没有成功走 t 的最后一位。

/**
 * @param {string} s
 * @param {string} t
 * @return {boolean}
 */
let isSubsequence = function (s, t) {
  let sl = s.length
  if (!sl) {
    return true
  }

  let i = 0
  for (let j = 0; j < t.length; j++) {
    let target = s[i]
    let cur = t[j]
    if (cur === target) {
      i++
      if (i === sl) {
        return true
      }
    }
  }

  return false
}

无重叠区间-435

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

示例 1:

输入: [ [1,2], [2,3], [3,4], [1,3] ]

输出: 1

解释: 移除 [1,3] 后，剩下的区间没有重叠。
示例 2:

输入: [ [1,2], [1,2], [1,2] ]

输出: 2

解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:

输入: [ [1,2], [2,3] ]

输出: 0

解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

来源：力扣（LeetCode） 链接：leetcode-cn.com/problems/non-overlapping-intervals 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

本题可以转化成最长上升子序列-300相同的问题。

先把区间数组按照每个数组的开头项排序，然后用 dp[i] 表示从 [0, i] 能构成的最长的无重叠区间的个数，利用上升子序列的同样思路去求解即可。对于每个区间intervals[i]，都从 0 ~ j 去逐个遍历之前的项，一旦发现 i.start >= j.end 说明这两者构成非重叠区间，那么就把 max 值尝试更新为 dp[j] + 1。

最后找出所有 dp 项中的最大值，也就是最长的非重叠区间长度，用区间的总长度减去这个最长长度，得出的就是需要移除掉的数组长度。

/**
 * @param {number[][]} intervals
 * @return {number}
 */
let eraseOverlapIntervals = function (intervals) {
  let n = intervals.length
  if (!n) {
    return 0
  }

  // 按照起始点排序
  intervals.sort((a, b) => a[0] - b[0])

  // dp[i] 表示从 [0, i] 能构成的最长的无重叠区间的个数
  let dp = []
  dp[0] = 1

  for (let i = 1; i < n; i++) {
    let max = 1
    let [curStart] = intervals[i]
    for (let j = 0; j < i; j++) {
      let [prevStart, prevEnd] = intervals[j]
      if (prevEnd <= curStart) {
        max = Math.max(max, dp[j] + 1)
      }
    }
    dp[i] = max
  }

  return n - Math.max(...dp)
}

字节面试算法题

一.字符串

1.1.无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

思路

我们需要找出一个字符串中 没有重复字符 的最长子串的长度。为了实现这一点，我们可以通过使用滑动窗口的技巧来解决：

• 使用两个指针：start 和 end，start 指向窗口的起始位置，end 指向窗口的结束位置。
• 使用一个集合（或哈希表）来记录当前窗口中的字符，确保窗口中没有重复字符。
• 每次移动 end 指针，检查窗口中是否存在重复字符。如果存在重复字符，则移动 start 指针，直到窗口中不再有重复字符。
• 在此过程中，不断更新最长无重复字符子串的长度。

/**
 * @param {string} s
 * @return {number}
 */
var lengthOfLongestSubstring = function (s) {
  let start = 0 // 窗口的起始位置
  let maxLength = 0 // 存储最长无重复字串的长度
  let set = new Set() // 存储当前窗口内的字符

  // 遍历字符串
  for (let end = 0; end < s.length; end++) {
    // 如果当前字符已经在窗口中，移动start指针
    while (set.has(s[end])) {
      set.delete(s[start]) // 删除窗口左边的字符
      start++ // 移动窗口起始位置
    }

    // 添加当前字符到窗口
    set.add(s[end])

    // 更新最大长度
    maxLength = Math.max(maxLength, end - start + 1)
  }

  return maxLength
}

1.2. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1：

输入：strs = ["flower","flow","flight"]
输出："fl"

示例 2：

输入：strs = ["dog","racecar","car"]
输出：""
解释：输入不存在公共前缀。

思路

1. 水平扫描法：
   • 假设公共前缀为第一个字符串 prefix。
   • 遍历数组的每个字符串，如果当前字符串不以 prefix 为前缀，就缩短 prefix，直到找到公共前缀或为空。
   • 时间复杂度取决于字符串的长度总和。

/**
 * @param {string[]} strs
 * @return {string}
 */
var longestCommonPrefix = function (strs) {
  if (!strs.length) return ''

  // 初始化公共前缀为第一个字符串
  let prefix = strs[0]

  // 遍历字符串数组
  for (let i = 1; i < strs.length; i++) {
    // 不断缩短prefix 直到成为当前字符串的前缀
    while (strs[i].indexOf(prefix) !== 0) {
      prefix = prefix.slice(0, -1)
      if (prefix === '') return ''
    }
  }

  return prefix
}

1.3.字符串的排列

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的 排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的 子串 。

示例 1：

输入：s1 = "ab" s2 = "eidbaooo"
输出：true
解释：s2 包含 s1 的排列之一 ("ba").

示例 2：

输入：s1= "ab" s2 = "eidboaoo"
输出：false

思路

1. 排列的特点：
   • 如果 s2 包含 s1 的一个排列，那么 s2 中存在一个子串，与 s1 的字符种类和频次完全相同。
2. 滑动窗口法：
   • 使用两个频率数组 need 和 window 来记录 s1 和当前窗口内的字符频率。
   • 遍历 s2，维护一个长度为 s1.length 的滑动窗口：
     • 窗口右移时，更新频率数组。
     • 如果窗口长度超出 s1.length，缩小窗口，移除最左字符。
   • 在每次窗口调整后，比较两个频率数组是否相等，若相等，则返回 true。

/**
 * @param {string} s1
 * @param {string} s2
 * @return {boolean}
 */
var checkInclusion = function (s1, s2) {
  const n = s1.length,
    m = s2.length
  if (n > m) return false

  // 记录 s1 的字符频率
  const need = new Array(26).fill(0)
  const window = new Array(26).fill(0)
  for (const char of s1) {
    need[char.charCodeAt(0) - 'a'.charCodeAt(0)]++
  }

  // 滑动窗口遍历 s2
  for (let i = 0; i < m; i++) {
    // 添加当前字符到窗口
    window[s2[i].charCodeAt(0) - 'a'.charCodeAt(0)]++

    // 如果窗口大小超过 s1 的长度，缩小窗口
    if (i >= n) {
      window[s2[i - n].charCodeAt(0) - 'a'.charCodeAt(0)]--
    }

    // 判断窗口内的字符频率是否匹配
    if (window.toString() === need.toString()) {
      return true
    }
  }

  return false
}

1.4.字符串相乘

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

**注意：**不能使用任何内置的 BigInteger 库或直接将输入转换为整数。

示例 1:

输入: num1 = "2", num2 = "3"
输出: "6"

示例 2:

输入: num1 = "123", num2 = "456"
输出: "56088"

提示：

• 1 <= num1.length, num2.length <= 200
• num1 和 num2 只能由数字组成。
• num1 和 num2 都不包含任何前导零，除了数字0本身。

思路

1. 初始化结果数组：
   • 使用一个长度为 num1.length + num2.length 的数组 res 来存储每一位的计算结果。原因是两个数字相乘，结果的位数最多是两者位数之和。
2. 从低位到高位模拟乘法：
   • 从 num1 和 num2 的最低位开始，两位相乘，把结果加到 res 的对应位置上。
3. 处理进位：
   • 遍历 res 数组，处理每一位上的进位。
4. 去除前导零：
   • 如果结果数组的高位是 0，需要去掉，直到保留至少一位。
5. 转换结果：
   • 将 res 数组转为字符串返回。

/**
 * @param {string} num1
 * @param {string} num2
 * @return {string}
 */
var multiply = function (num1, num2) {
  if (num1 === '0' || num2 === '0') return '0'

  const m = num1.length
  const n = num2.length
  const res = new Array(m + n).fill(0)

  // 从低位到高位逐位相乘
  for (let i = m - 1; i >= 0; i--) {
    for (let j = n - 1; j >= 0; j--) {
      const mul = (num1[i] - '0') * (num2[j] - '0')
      const p1 = i + j
      const p2 = i + j + 1

      // 加到对应位置
      const sum = mul + res[p2]
      res[p2] = sum % 10 // 当前位
      res[p1] += Math.floor(sum / 10) // 进位
    }
  }

  // 去除前导零
  let result = res.join('')
  while (result[0] === '0') {
    result = result.slice(1)
  }

  return result
}

1.5.反转字符串中的单词

给你一个字符串 s ，请你反转字符串中 单词 的顺序。

单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。

返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。

**注意：**输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。

示例 1：

输入：s = "the sky is blue"
输出："blue is sky the"

示例 2：

输入：s = "  hello world  "
输出："world hello"
解释：反转后的字符串中不能存在前导空格和尾随空格。

示例 3：

输入：s = "a good   example"
输出："example good a"
解释：如果两个单词间有多余的空格，反转后的字符串需要将单词间的空格减少到仅有一个。

提示：

• 1 <= s.length <= 104
• s 包含英文大小写字母、数字和空格 ' '
• s 中 至少存在一个 单词

思路

要将字符串中的单词顺序反转，同时规范空格的使用，可以分以下几步实现：

1. 移除多余空格：
   • 去掉字符串的前导和尾随空格。
   • 将单词之间的多个空格缩减为一个。
2. 分割单词：
   • 使用空格分割字符串成单词列表。
3. 反转单词列表：
   • 使用数组的反转功能将单词顺序颠倒。
4. 重新拼接字符串：
   • 用单个空格将反转后的单词列表拼接成字符串。

/**
 * @param {string} s
 * @return {string}
 */
var reverseWords = function (s) {
  // 去除多余空格并分割单词
  const words = s.trim().split(/\s+/)
  // 反转单词列表并拼接成结果字符串
  return words.reverse().join(' ')
}

1.6.简化路径

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为 更加简洁的规范路径。

在 Unix 风格的文件系统中规则如下：

• 一个点 '.' 表示当前目录本身。
• 此外，两个点 '..' 表示将目录切换到上一级（指向父目录）。
• 任意多个连续的斜杠（即，'//' 或 '///'）都被视为单个斜杠 '/'。
• 任何其他格式的点（例如，'...' 或 '....'）均被视为有效的文件/目录名称。

返回的 简化路径 必须遵循下述格式：

• 始终以斜杠 '/' 开头。
• 两个目录名之间必须只有一个斜杠 '/' 。
• 最后一个目录名（如果存在）不能 以 '/' 结尾。
• 此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

返回简化后得到的 规范路径 。

示例 1：

**输入：**path = "/home/"

输出："/home"

解释：

应删除尾随斜杠。

示例 2：

**输入：**path = "/home//foo/"

输出："/home/foo"

解释：

多个连续的斜杠被单个斜杠替换。

示例 3：

**输入：**path = "/home/user/Documents/../Pictures"

输出："/home/user/Pictures"

解释：

两个点 ".." 表示上一级目录（父目录）。

示例 4：

**输入：**path = "/../"

输出："/"

解释：

不可能从根目录上升一级目录。

示例 5：

**输入：**path = "/.../a/../b/c/../d/./"

输出："/.../b/d"

解释：

"..." 在这个问题中是一个合法的目录名。

提示：

• 1 <= path.length <= 3000
• path 由英文字母，数字，'.'，'/' 或 '_' 组成。
• path 是一个有效的 Unix 风格绝对路径。

思路

要将 Unix 风格路径简化为规范路径，可以使用栈数据结构逐步处理路径组件。简化过程如下：

1. 路径分割：
   • 使用 '/' 分割路径，将其分解为路径片段。
   • 忽略空片段（由多个斜杠导致）和 .（表示当前目录）。
2. 路径简化：
   • 如果路径片段为 ..，表示返回上一级目录：
     • 如果栈不为空，则弹出栈顶元素。
   • 如果路径片段为合法的目录名（非 . 或 ..），将其压入栈中。
3. 结果拼接：
   • 最终栈中的元素表示简化路径的各部分。
   • 用 '/' 拼接栈中元素，并在开头添加根路径 '/'。
4. 特殊情况：
   • 如果路径为空或最终栈为空，返回根路径 '/'。

/**
 * @param {string} path
 * @return {string}
 */
var simplifyPath = function (path) {
  const stack = []
  const components = path.split('/')

  for (const component of components) {
    if (component === '..') {
      if (stack.length > 0) {
        stack.pop()
      }
    } else if (component !== '' && component !== '.') {
      stack.push(component)
    }
  }

  return '/' + stack.join('/')
}

1.7.复原 IP 地址

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

• 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

• 1 <= s.length <= 20
• s 仅由数字组成

思路

题目要求生成所有可能的有效 IP 地址，我们可以使用回溯法来解决。具体思路如下：

1. 回溯核心逻辑：
   • 每个 IP 地址由 4 段组成，每段的长度为 1~3，数值在-~255 范围内。
   • 遍历每个可能的分割位置，将字符串分成当前段和剩余部分，递归处理剩余部分。
   • 如果当前段合法且递归完成后剩下 4 段，则构成一个有效 IP 地址。
2. 合法性判断：
   • 每段不能有前导 0（除非该段是单独的 0）。
   • 每段的数值必须在 [0, 255] 范围内。
3. 终止条件：
   • 当构造的 IP 地址段数为 4 且用完所有字符时，将其加入结果集。
   • 如果段数超过 4 或字符串未用完但段数已满，回溯终止。

/**
 * @param {string} s
 * @return {string[]}
 */
var restoreIpAddresses = function (s) {
  const result = []
  const path = []

  // 检查每段是否合法
  function isValid(segment) {
    if (segment.length > 1 && segment[0] === '0') return false // 前导0
    const num = parseInt(segment, 10)
    return num >= 0 && num <= 255
  }

  // 回溯函数
  function backtrack(start) {
    if (path.length === 4) {
      // 如果刚好用完所有字符，添加到结果集
      if (start === s.length) {
        result.push(path.join('.'))
      }
      return
    }

    // 尝试每段的长度为 1~3
    for (let len = 1; len <= 3; len++) {
      if (start + len > s.length) break // 超出字符串长度
      const segment = s.slice(start, start + len)
      if (isValid(segment)) {
        path.push(segment) // 做选择
        backtrack(start + len) // 递归
        path.pop() // 撤销选择
      }
    }
  }

  backtrack(0)
  return result
}

二.数组与排序

2.1. 三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

提示：

• 3 <= nums.length <= 3000
• -105 <= nums[i] <= 105

思路

1. 排序数组：
   • 对数组进行从小到大的排序，方便后续使用双指针。
2. 固定一个数，寻找剩余两数：
   • 遍历数组，固定第一个数 nums[i]。
   • 对于剩下的部分，使用双指针法寻找两数之和为 −nums[i]。
3. 双指针法：
   • 使用两个指针 left 和 right，分别指向当前区间的头尾。
   • 根据三数之和 nums[i]+nums[left]+nums[right]
     • 如果和小于 0，则 left++ 以增加总和。
     • 如果和大于 0，则 right−− 以减少总和。
     • 如果等于 0，则记录结果，同时跳过重复元素。
4. 去重：
   • 遍历过程中跳过重复的固定数 nums[i] 和指针指向的重复元素 nums[left],nums[right]。
5. 终止条件：
   • 双指针在区间内交错时停止搜索。

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var threeSum = function (nums) {
  const result = []
  nums.sort((a, b) => a - b) // 排序

  for (let i = 0; i < nums.length - 2; i++) {
    if (i > 0 && nums[i] === nums[i - 1]) continue // 跳过重复的固定数

    let left = i + 1,
      right = nums.length - 1
    while (left < right) {
      const sum = nums[i] + nums[left] + nums[right]
      if (sum === 0) {
        result.push([nums[i], nums[left], nums[right]])
        left++
        right--
        // 跳过重复的左指针和右指针
        while (left < right && nums[left] === nums[left - 1]) left++
        while (left < right && nums[right] === nums[right + 1]) right--
      } else if (sum < 0) {
        left++ // 总和小于 0，移动左指针
      } else {
        right-- // 总和大于 0，移动右指针
      }
    }
  }

  return result
}

2.2.岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] 为 0 或 1

思路

题目要求计算二进制矩阵中最大的岛屿面积，岛屿由水平或垂直相邻的 1 组成。这可以通过 深度优先搜索 (DFS) 或 广度优先搜索 (BFS) 来实现。

1. 遍历矩阵：
   • 遍历矩阵的每个单元格，如果当前单元格的值是 1，表示发现了一个新的岛屿。
2. 递归或迭代搜索：
   • 使用 DFS 或 BFS 搜索岛屿的所有相邻单元格，将它们的值标记为 0（防止重复计算）。
   • 计算当前岛屿的面积。
3. 记录最大面积：
   • 在搜索的过程中，记录每个岛屿的面积并更新最大值。
4. 边界处理：
   • 确保搜索不会超出矩阵范围。

DFS

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxAreaOfIsland = function (grid) {
  const m = grid.length
  const n = grid[0].length
  let maxArea = 0

  // 深度优先搜索函数
  function dfs(x, y) {
    if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] === 0) {
      return 0
    }
    grid[x][y] = 0 // 将访问过的土地标记为0
    let area = 1 // 当前单元格的面积为1

    // 搜索四个方向
    area += dfs(x - 1, y) // 上
    area += dfs(x + 1, y) // 下
    area += dfs(x, y - 1) // 左
    area += dfs(x, y + 1) // 右

    return area
  }

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === 1) {
        maxArea = Math.max(maxArea, dfs(i, j))
      }
    }
  }

  return maxArea
}

BFS

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxAreaOfIsland = function (grid) {
  const m = grid.length
  const n = grid[0].length
  let maxArea = 0

  function bfs(x, y) {
    const queue = [[x, y]]
    let area = 0

    while (queue.length > 0) {
      const [cx, cy] = queue.shift()
      if (cx < 0 || cx >= m || cy < 0 || cy >= n || grid[cx][cy] === 0) {
        continue
      }

      grid[cx][cy] = 0 // 将访问过的土地标记为0
      area++

      // 添加相邻的四个方向
      queue.push([cx - 1, cy]) // 上
      queue.push([cx + 1, cy]) // 上
      queue.push([cx, cy - 1]) // 上
      queue.push([cx, cy + 1]) // 上
    }

    return area
  }

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === 1) {
        maxArea = Math.max(maxArea, bfs(i, j))
      }
    }
  }

  return maxArea
}

2.3.搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

思路分析

1. 数组特点：
   • 数组是升序排列后旋转的，其中一部分仍然是有序的。
   • 通过判断中点值，可以确定哪一部分是有序的。
2. 二分查找过程：
   • 确定有序区间：比较中间值与左右边界值，判断是左半部分有序还是右半部分有序。
   • 目标值是否在有序区间内：根据目标值与边界值的关系判断。
   • 缩小范围：调整左边界或右边界。

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function (nums, target) {
  let left = 0
  let right = nums.length - 1

  while (left <= right) {
    const mid = Math.floor((left + right) / 2)

    if (nums[mid] === target) {
      return mid
    }

    // 判断左半部分是否有序
    if (nums[left] <= nums[mid]) {
      // 判断目标值是否在左半部分
      if (nums[left] <= target && target < nums[mid]) {
        right = mid - 1
      } else {
        left = mid + 1
      }
    } else {
      // 右半部分有序
      if (nums[mid] < target && target <= nums[right]) {
        left = mid + 1
      } else {
        right = mid - 1
      }
    }
  }

  return -1 // 未找到目标值
}

2.4.最长连续递增序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

• 1 <= nums.length <= 104
• -109 <= nums[i] <= 109

思路

这道题要求找到 最长连续递增子序列 的长度，关键是：

1. 子序列必须是连续的。
2. 数组是无序的，需要逐一检查每对相邻元素的关系。

采用一次遍历解决问题，通过维护两个变量：

• 当前长度 (currentLength)：记录当前连续递增序列的长度。
• 最大长度 (maxLength)：记录找到的最长连续递增序列的长度。

/**
 * @param {number[]} nums
 * @return {number}
 */
var findLengthOfLCIS = function (nums) {
  if (nums.length === 0) return 0

  let maxLength = 1
  let currentLength = 1

  for (let i = 1; i < nums.length; i++) {
    if (nums[i] > nums[i - 1]) {
      currentLength++
    } else {
      maxLength = Math.max(maxLength, currentLength)
      currentLength = 1
    }
  }

  // 更新最后的最大长度
  return Math.max(maxLength, currentLength)
}

2.5.数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

提示：

• 1 <= k <= nums.length <= 105
• -104 <= nums[i] <= 104

方法：快速选择算法（Quickselect）

快速选择算法是从快速排序演变而来的，核心思想是利用 分区操作 在未完全排序的数组中找到目标位置的元素。它的平均时间复杂度是 O(n)，最坏情况下是 O(n²)。

分区操作：

• 随机选择一个枢轴（pivot）。
• 将数组分为两部分：
  • 左边部分的元素大于等于枢轴。
  • 右边部分的元素小于枢轴。

判断位置：

• 如果分区后的枢轴位置正好是目标索引（即第 k 大元素的索引），返回枢轴值。
• 如果目标索引在左边部分，递归左子数组。
• 如果目标索引在右边部分，递归右子数组。

终止条件：

• 当数组长度为 1 或找到目标位置时，直接返回结果。

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function (nums, k) {
  const n = nums.length
  const targetIndex = n - k // 转换为寻找第 n-k 小的元素

  const partition = (left, right) => {
    const pivot = nums[right] // 选择最右边的元素作为枢轴
    let i = left
    for (let j = left; j < right; j++) {
      if (nums[j] <= pivot) {
        ;[nums[i], nums[j]] = [nums[j], nums[i]]
        i++
      }
    }
    ;[nums[i], nums[right]] = [nums[right], nums[i]] // 将枢轴放到正确位置
    return i
  }

  let left = 0,
    right = n - 1
  while (left <= right) {
    const pivotIndex = partition(left, right)
    if (pivotIndex === targetIndex) {
      return nums[pivotIndex]
    } else if (pivotIndex < targetIndex) {
      left = pivotIndex + 1
    } else {
      right = pivotIndex - 1
    }
  }
}

hash 空间换时间

var findKthLargest = function (nums, k) {
  // 找到数组中的最大元素
  let largest = -Infinity

  for (let i = 0; i < nums.length; i++) {
    if (nums[i] > largest) largest = nums[i]
  }

  // 构建一个哈希表，记录每个元素与最大值的差
  const hash = {}

  for (let i = 0; i < nums.length; i++) {
    const diff = largest - nums[i]
    hash[diff] = (hash[diff] || 0) + 1 // 记录差值出现的次数
  }

  // 找到第 k 大的元素
  let count = 0
  let diff = 0
  while (count < k) {
    count += hash[diff] || 0 // 累加当前差值的出现次数
    diff++
  }

  return largest - diff + 1 // 返回第 k 大的元素
}

2.6.最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109

思路

1. 使用哈希集合
   • 将所有数字存入一个哈希集合 Set，以便在 O(1) 时间内检查某个数字是否存在。
2. 寻找连续序列的起点
   • 只有当某个数字是序列的起点（即 num - 1 不在集合中）时，才开始计算该序列的长度。
3. 计算连续序列长度
   • 对于每个序列起点，逐步检查后续数字是否存在，并记录序列长度。
4. 更新最长长度
   • 在所有序列中，记录最长的序列长度。

/**
 * @param {number[]} nums
 * @return {number}
 */
var longestConsecutive = function (nums) {
  const numSet = new Set(nums) // 创建哈希集合
  let maxLength = 0

  for (const num of numSet) {
    // 如果是连续序列的起点
    if (!numSet.has(num - 1)) {
      let currentNum = num
      let currentLength = 1

      // 不断查找下一个数字
      while (numSet.has(currentNum + 1)) {
        currentNum++
        currentLength++
      }

      // 更新最长长度
      maxLength = Math.max(maxLength, currentLength)
    }
  }

  return maxLength
}

2.7.排列序列

给出集合 [1,2,3,...,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"

给定 n 和 k，返回第 k 个排列。

示例 1：

输入：n = 3, k = 3
输出："213"

示例 2：

输入：n = 4, k = 9
输出："2314"

示例 3：

输入：n = 3, k = 1
输出："123"

提示：

• 1 <= n <= 9
• 1 <= k <= n!

思路

1. 阶乘数组
   • 预先计算阶乘 factorial[i]，表示 n!，用于确定当前位置的选择范围。
2. 数字选择
   • 从高位到低位，依次确定当前位的数字。
   • 对于第 i 位，使用 k 除以 (n−i)!(n-i)!(n−i)! 得到当前数字的索引。
   • 更新 k 的值为 k mod  (n−i)!，继续处理下一位。
3. 标记已使用数字
   • 通过一个数组或集合记录已使用的数字，确保每次选择的数字不重复。

/**
 * @param {number} n
 * @param {number} k
 * @return {string}
 */
var getPermutation = function (n, k) {
  // 计算阶乘数组
  const factorial = [1]
  for (let i = 1; i <= n; i++) {
    factorial[i] = factorial[i - 1] * i
  }

  // 初始化可选数字列表
  const nums = Array.from({ length: n }, (_, i) => i + 1)
  k-- // 将 k 转换为 0 索引

  let result = ''

  for (let i = 1; i <= n; i++) {
    // 计算当前位数字的索引
    const index = Math.floor(k / factorial[n - i])
    result += nums[index]
    // 删除已选数字
    nums.splice(index, 1)
    // 更新 k
    k %= factorial[n - i]
  }

  return result
}

2.8.省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

思路：深度优先搜索（DFS）

1. 将 isConnected 矩阵看作图的邻接矩阵。
2. 使用一个布尔数组 visited 记录每个城市是否已经访问过。
3. 遍历每个城市：
   • 如果城市未被访问，则启动一次 DFS，访问所有与该城市直接或间接相连的城市。
   • 每次启动 DFS 都意味着发现了一个新的省份。
4. 返回省份数量。

/**
 * @param {number[][]} isConnected
 * @return {number}
 */
var findCircleNum = function (isConnected) {
  const n = isConnected.length
  const visited = Array(n).fill(false)
  let provinces = 0

  const dfs = (i) => {
    visited[i] = true
    for (let j = 0; j < n; j++) {
      if (isConnected[i][j] === 1 && !visited[j]) {
        dfs(j)
      }
    }
  }

  for (let i = 0; i < n; i++) {
    if (!visited[i]) {
      provinces++
      dfs(i)
    }
  }

  return provinces
}

2.9.合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

• 1 <= intervals.length <= 104
• intervals[i].length == 2
• 0 <= starti <= endi <= 104

思路

1. 排序区间：
   • 首先，我们需要按区间的起始值对所有区间进行排序。排序的目的是保证合并时，能够顺序地判断哪些区间是重叠的，哪些不是。
2. 合并区间：
   • 遍历排序后的区间，检查当前区间与已合并的区间是否重叠。
   • 如果当前区间的起始值大于已合并区间的结束值，说明不重叠，直接将当前区间加入结果。
   • 如果当前区间与已合并区间重叠，我们将这两个区间合并，新的合并区间的起始值是原来两个区间的起始值较小者，结束值是原来两个区间的结束值较大者。

/**
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function (intervals) {
  // 1.按区间的起始值排序
  intervals.sort((a, b) => a[0] - b[0])

  const merged = []

  for (let interval of intervals) {
    // 2.如果merged为空或者当前区间和merged中的最后一个区间不重叠，直接添加
    if (merged.length === 0 || merged[merged.length - 1][1] < interval[0]) {
      merged.push(interval)
    } else {
      // 3.如果重叠，合并区间
      merged[merged.length - 1][1] = Math.max(
        merged[merged.length - 1][1],
        interval[1]
      )
    }
  }

  return merged
}

2.9.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

思路：双指针法

1. 使用两个指针 left 和 right 从两端向中间移动。
2. 维护两个变量 leftMax 和 rightMax，分别记录当前左右指针的最大高度。
3. 比较 leftMax 和 rightMax，高度较小的一侧决定能存储的雨水量。

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
  if (height.length === 0) return 0

  let left = 0
  let right = height.length - 1
  let leftMax = 0
  let rightMax = 0
  let water = 0

  while (left <= right) {
    if (height[left] < height[right]) {
      // 左侧较低
      if (height[left] >= leftMax) {
        leftMax = height[left]
      } else {
        water += leftMax - height[left]
      }
      left++
    } else {
      // 右侧较低
      if (height[right] >= rightMax) {
        rightMax = height[right]
      } else {
        water += rightMax - height[right]
      }
      right--
    }
  }

  return water
}

三.链表和树

3.1.合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

• 两个链表的节点数目范围是 [0, 50]
• -100 <= Node.val <= 100
• l1 和 l2 均按 非递减顺序 排列

思路

题目要求将两个升序链表合并为一个新的升序链表，并返回新的链表。这个问题可以通过双指针法来高效解决。

• 合并规则：每次比较两个链表的当前节点，将较小的节点加入到新链表中，继续比较。
• 最终，我们只需要将两个链表中的元素逐个插入到新的链表中，直到遍历完其中一个链表。然后，将另一个链表中剩余的部分直接连接到新链表的末尾。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} list1
 * @param {ListNode} list2
 * @return {ListNode}
 */
var mergeTwoLists = function (l1, l2) {
  // 创建一个虚拟的头节点，简化链表操作
  let dummy = new ListNode(-1)
  let current = dummy // 当前指针

  // 双指针法遍历两个链表
  while (l1 !== null && l2 !== null) {
    if (l1.val < l2.val) {
      current.next = l1
      l1 = l1.next
    } else {
      current.next = l2
      l2 = l2.next
    }
    current = current.next // 移动current指针
  }

  // 如果l1或l2中还有剩余节点，直接连接到新链表末尾
  if (l1 !== null) {
    current.next = l1
  } else if (l2 !== null) {
    current.next = l2
  }

  // 返回合并后的链表（跳过虚拟头节点）
  return dummy.next
}

3.2.反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

思路

反转链表的基本思想是通过遍历链表并逐步改变每个节点的指针方向。我们可以使用三指针方法来实现链表的反转：

1. 当前节点（cur）：指向当前正在处理的节点。
2. 前驱节点（prev）：指向当前节点的前一个节点，初始时为null。
3. 后继节点（next）：指向当前节点的下一个节点，用于保存当前节点的后继，以便在修改指针时不会丢失链表的后续部分。

反转链表的步骤：

1. 遍历链表，取出当前节点的后继节点。
2. 将当前节点的 next 指向前驱节点。
3. 更新前驱节点和当前节点为后续节点。

当遍历完成后，链表的头节点就会是原链表的尾节点，反转完成。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function (head) {
  let prev = null // 初始化前驱节点为空
  let cur = head // 当前节点指向头节点

  while (cur !== null) {
    let nextTemp = cur.next // 保存当前节点的后继节点
    cur.next = prev // 将当前节点的next指向前驱节点
    prev = cur // 前驱节点更新为当前节点
    cur = nextTemp // 当前节点更新为后继节点
  }

  return prev
}

3.3.两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

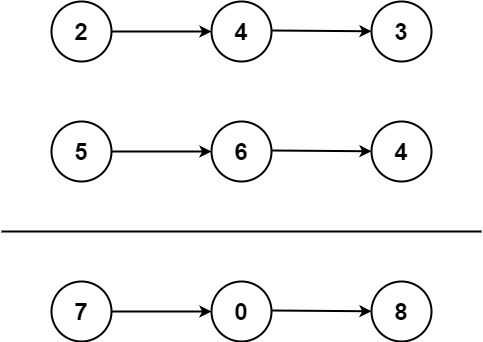
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

思路

我们可以逐位进行加法。具体步骤如下：

1. 初始化：设置一个进位 carry 为 0，表示每次相加可能会有进位。
2. 逐位相加
   • 从两个链表的头节点开始，依次取出每一位的数字进行相加。
   • 每次相加时，考虑进位，将结果存储在新链表的当前节点。
   • 如果两链表的长度不同，需要处理较短链表的“虚拟节点”。
3. 处理进位：如果最终有进位（即 carry 不为 0），则需要创建一个新的节点存储进位。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
var addTwoNumbers = function (l1, l2) {
  let dummyHead = new ListNode(0) // 用一个虚拟头结点，方便返回结果
  let current = dummyHead // 当前指针，用来连接新节点
  let carry = 0 // 进位

  // 遍历两个链表，直到两个链表都为空，或者进位为0
  while (l1 !== null || l2 !== null || carry !== 0) {
    let sum = carry // 先加上进位

    if (l1 !== null) {
      sum += l1.val // 加上l1的当前节点的值
      l1 = l1.next // 移动到l1的下一个节点
    }

    if (l2 !== null) {
      sum += l2.val // 加上l2的当前节点的值
      l2 = l2.next // 移动到l2的下一个节点
    }

    carry = Math.floor(sum / 10) // 计算新的进位
    current.next = new ListNode(sum % 10) // 生产当前位的节点
    current = current.next // 移动当前节点指针
  }

  return dummyHead.next // 返回结果链表，跳过虚拟头节点
}

3.4.排序链表

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：

输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

输入：head = []
输出：[]

思路

链表适合使用 归并排序，因为：归并排序可以在链表中原地进行，不需要额外的数组存储。链表的随机访问复杂度较高，而归并排序不依赖于随机访问。

1. 使用快慢指针将链表分成两部分。
2. 递归地对两部分链表进行排序。
3. 将两个有序链表合并成一个新的有序链表。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var sortList = function (head) {
  if (!head || !head.next) {
    return head // 空链表或只有一个节点时，直接返回
  }

  // 使用快慢指针找到链表中点
  let slow = head
  let fast = head
  let prev = null

  while (fast && fast.next) {
    prev = slow
    slow = slow.next
    fast = fast.next.next
  }
  prev.next = null // 将链表断开

  // 对左右两部分链表排序
  let left = sortList(head)
  let right = sortList(slow)

  // 合并两个有序链表
  return mergeTwoLists(left, right)
}

var mergeTwoLists = function (l1, l2) {
  let dummyHead = new ListNode(0)
  let current = dummyHead

  while (l1 && l2) {
    if (l1.val <= l2.val) {
      current.next = l1
      l1 = l1.next
    } else {
      current.next = l2
      l2 = l2.next
    }
    current = current.next
  }

  current.next = l1 || l2 // 连接剩余部分
  return dummyHead.next
}

3.5.环形链表 II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

思路

1. 使用快慢指针判断链表是否有环：
   • 快指针每次走两步，慢指针每次走一步。
   • 如果链表有环，快慢指针会在环中某节点相遇。
2. 如果有环，找到环的起始节点：
   • 从链表头和相遇点分别开始移动，每次移动一步。
   • 两个指针最终会在环的起始节点相遇。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function (head) {
  if (!head || !head.next) return null

  let slow = head
  let fast = head

  // 判断是否有环
  while (fast && fast.next) {
    slow = slow.next
    fast = fast.next.next
    if (slow === fast) {
      // 有环，寻找环的起始节点
      let pointer1 = head
      let pointer2 = slow
      while (pointer1 !== pointer2) {
        pointer1 = pointer1.next
        pointer2 = pointer2.next
      }
      return pointer1
    }
  }

  return null // 无环
}

3.6.相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交**：**

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

• intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
• listA - 第一个链表
• listB - 第二个链表
• skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
• skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：No intersection
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

思路

1. 计算链表长度：
   • 遍历链表 headA 和 headB，分别计算它们的长度 lenA 和 lenB。
2. 对齐起点：
   • 计算长度差 diff = |lenA - lenB|。
   • 较长的链表先移动 diff 步，使得两链表从相同的距离开始对齐遍历。
3. 寻找相交节点：
   • 同时遍历两链表，比较当前节点是否相同（内存地址是否相同）。
   • 如果找到相同节点，则返回；如果遍历结束没有找到，则返回 null。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} headA
 * @param {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function (headA, headB) {
  if (!headA || !headB) return null

  // 计算链表A的长度
  let lenA = 0
  let lenB = 0
  let currA = headA
  let currB = headB

  while (currA) {
    lenA++
    currA = currA.next
  }

  // 计算链表B的长度
  while (currB) {
    lenB++
    currB = currB.next
  }

  // 对齐链表起点
  currA = headA
  currB = headB
  if (lenA > lenB) {
    for (let i = 0; i < lenA - lenB; i++) {
      currA = currA.next
    }
  } else {
    for (let i = 0; i < lenB - lenA; i++) {
      currB = currB.next
    }
  }

  // 同时遍历两个链表，找到相交节点
  while (currA && currB) {
    if (currA === currB) {
      return currA
    }
    currA = currA.next
    currB = currB.next
  }

  return null // 未找到相交节点
}

3.7.给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

思路

1. 分治法：
   • 两两合并链表，直到只剩一个链表。
   • 每次合并两个链表使用归并的方式，这样可以减少总的比较次数。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function (lists) {
  if (!lists || lists.length === 0) return null

  const mergeTwoLists = (l1, l2) => {
    let dummy = new ListNode(-1)
    let current = dummy

    while (l1 && l2) {
      if (l1.val < l2.val) {
        current.next = l1
        l1 = l1.next
      } else {
        current.next = l2
        l2 = l2.next
      }
      current = current.next
    }

    current.next = l1 || l2
    return dummy.next
  }

  const merge = (lists, start, end) => {
    if (start === end) return lists[start]
    const mid = Math.floor((start + end) / 2)
    const left = merge(lists, start, mid)
    const right = merge(lists, mid + 1, end)
    return mergeTwoLists(left, right)
  }

  return merge(lists, 0, lists.length - 1)
}

3.8.二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

思路

要找二叉树中两个节点的最近公共祖先，常用递归方法。 主要思路是：

1. 如果当前节点是 null，返回 null。
2. 如果当前节点是 p 或 q，返回当前节点。
3. 递归地在左右子树中查找 p 和 q
   • 如果 p 和 q 分别出现在左右子树中，当前节点就是最近公共祖先。
   • 如果 p 和 q 都在左子树或都在右子树，则继续递归查找。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  if (!root || root === p || root === q) return root

  const left = lowestCommonAncestor(root.left, p, q)
  const right = lowestCommonAncestor(root.right, p, q)

  if (left && right) return root // p 和 q 分别在左右字数
  return left || right // p 和 q 都在一侧
}

3.9.二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

思路

锯齿形层序遍历本质上是普通层序遍历的扩展，核心思想是：

1. 使用队列进行层序遍历。
2. 每层结束时，根据当前层数的奇偶性决定将节点值从左到右或从右到左加入结果列表。
3. 使用一个变量 isLeftToRight 标记当前层的遍历方向，并在每层结束后切换方向。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var zigzagLevelOrder = function (root) {
  if (!root) return []

  const result = []
  const queue = [root]
  let isLeftToRight = true // 标记遍历方向

  while (queue.length > 0) {
    const levelSize = queue.length
    const currentLevel = []

    for (let i = 0; i < levelSize; i++) {
      const node = queue.shift()

      // 根据方向决定插入位置
      if (isLeftToRight) {
        currentLevel.push(node.val)
      } else {
        currentLevel.unshift(node.val)
      }

      // 将子节点加入队列
      if (node.left) queue.push(node.left)
      if (node.right) queue.push(node.right)
    }

    result.push(currentLevel)
    isLeftToRight = !isLeftToRight // 切换方向
  }

  return result
}

四.动态或贪心

4.1.买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

思路

本题需要在一个数组中找到两天的价格差（先买后卖），使得利润最大。我们可以使用一个简单的遍历算法实现该功能：

1. 用一个变量 minPrice 保存遍历过程中遇到的最小股票价格。
2. 用一个变量 maxProfit 保存当前可以获得的最大利润。
3. 遍历数组：
   • 对于每一天，计算当天价格与 minPrice 的差值，更新 maxProfit。
   • 更新 minPrice 为当前的最低价格。

通过一次遍历即可完成，时间复杂度为 O(n)。

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function (prices) {
  if (prices.length === 0) return 0

  let minPrice = Infinity // 初始化为正无穷大
  let maxProfit = 0

  for (let price of prices) {
    // 更新最小价格
    if (price < minPrice) {
      minPrice = price
    } else {
      // 更新最大利润
      maxProfit = Math.max(maxProfit, price - minPrice)
    }
  }

  return maxProfit
}

4.2.买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0。

思路

本题允许多次买卖股票，只要当天价格比前一天高，就可以获取利润。问题的本质是累加 所有上涨区间 的差值。

关键点：

• 当价格从前一天到当前是上涨的，就将差值加入利润中。
• 遍历整个数组，累计所有的利润。

算法流程

1. 初始化变量 maxProfit 用于累计最大利润。
2. 遍历价格数组：
   • 如果当前价格比前一天高，则将差值加入 maxProfit。
3. 遍历完成后，返回 maxProfit。

该方法的时间复杂度为 O(n))，空间复杂度为 O(1)。

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function (prices) {
  let maxProfit = 0

  for (let i = 1; i < prices.length; i++) {
    if (prices[i] > prices[i - 1]) {
      maxProfit += prices[i] - prices[i - 1]
    }
  }

  return maxProfit
}

4.3.最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

思路

本题可以通过动态规划来解决，具体方法如下：

1. 状态定义

定义一个二维数组 dp，其中 dp[i][j] 表示以位置 (i, j) 为右下角的最大正方形的边长。

2. 状态转移方程

• 如果 matrix[i][j] == "1"，那么可以形成正方形。

• 状态转移方程为：dp[i][j]=min(dp[i−1][j],dp[i][j−1],dp[i−1][j−1])+1

  意思是，当前位置能形成的最大正方形边长等于它的上方、左方和左上方三个位置中最小的正方形边长 +1。

3. 初始化

• 如果 matrix[i][j] == "1" 且在矩阵边界（i == 0 或 j == 0），则 dp[i][j] = 1，因为边界上只能形成边长为 1 的正方形。
• 否则初始化为 0。

4. 结果

遍历整个 dp 数组，取其中的最大值作为最大正方形的边长，面积则为其平方。

/**
 * @param {character[][]} matrix
 * @return {number}
 */
var maximalSquare = function (matrix) {
  if (matrix.length === 0 || matrix[0].length === 0) return 0

  const rows = matrix.length
  const cols = matrix[0].length
  const dp = Array.from({ length: rows }, () => Array(cols).fill(0))
  let maxSize = 0

  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (matrix[i][j] === '1') {
        if (i === 0 || j === 0) {
          dp[i][j] = 1 // 边界情况
        } else {
          dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1
        }
        maxSize = Math.max(maxSize, dp[i][j]) // 更新最大边长
      }
    }
  }

  return maxSize * maxSize // 返回面积
}

4.4.最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

思路 （贪心）

1. 使用一个变量 currentSum 表示当前子数组的和。
2. 如果 currentSum 小于 0，则直接丢弃当前子数组，从下一个元素重新开始。
3. 使用另一个变量 maxSum 记录迄今为止的最大和。

/**
 * @param {number[]} nums
 * @return {number}
 */
var maxSubArray = function (nums) {
  let currentSum = 0
  let maxSum = nums[0] // 初始化最大值为第一个元素

  for (let num of nums) {
    currentSum = Math.max(num, currentSum + num) // 贪心决策
    maxSum = Math.max(maxSum, currentSum) // 更新最大值
  }

  return maxSum
}

4.5.三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

思路：

从一个三角形结构中找到从顶部到底部路径中相邻节点的最小路径和。每次只能移动到下一行中相邻的节点。

dp[i][j]=triangle[i][j]+min(dp[i+1][j],dp[i+1][j+1])

/**
 * @param {number[][]} triangle
 * @return {number}
 */
var minimumTotal = function (triangle) {
  const n = triangle.length

  // 从倒数第二行开始向上遍历每一行
  for (let i = n - 2; i >= 0; i--) {
    for (let j = 0; j < triangle[i].length; j++) {
      // 更新当前节点与相邻节点的最小路径和
      triangle[i][j] += Math.min(triangle[i + 1][j], triangle[i + 1][j + 1])
    }
  }

  return triangle[0][0] // 返回顶点的最小路径和
}

4.6.俄罗斯套娃信封问题

给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi] ，表示第 i 个信封的宽度和高度。

当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

注意：不允许旋转信封。

示例 1：

输入：envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

示例 2：

输入：envelopes = [[1,1],[1,1],[1,1]]
输出：1

思路：动态规划 + 最长上升子序列（LIS）

1. 排序： 首先，我们需要对 envelopes 进行排序。我们按以下规则对信封进行排序：

   • 按照宽度 w 升序排列。
   • 如果宽度相等，则根据高度 h 降序排列。

   这样可以保证当宽度相等时，较小的高度会放在后面，从而避免错误地将宽度相等但高度反转的信封放入。

2. 求最长上升子序列： 对排序后的高度进行求最长上升子序列。这个求 LIS 问题可以通过动态规划或二分法等高效方法求解。

var maxEnvelopes = function (envelopes) {
  // 1. 按宽度升序排序，如果宽度相等，则按高度降序排列
  envelopes.sort((a, b) => {
    if (a[0] !== b[0]) return a[0] - b[0]
    return b[1] - a[1]
  })

  const heights = envelopes.map((envelope) => envelope[1])
  const dp = []

  // 2. 使用二分法求解最长上升子序列
  for (let height of heights) {
    const idx = binarySearch(dp, height)
    dp[idx] = height
  }

  return dp.length
}

// 二分查找：找到第一个大于等于 target 的位置
function binarySearch(dp, target) {
  let left = 0,
    right = dp.length - 1
  while (left <= right) {
    const mid = Math.floor((left + right) / 2)
    if (dp[mid] < target) {
      left = mid + 1
    } else {
      right = mid - 1
    }
  }
  return left
}

五.数据结构

5.1.最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

思路：

我们可以通过维护两个栈来高效地实现上述操作：

1. 主栈 stack：
   • 存放所有元素。
2. 辅助栈 minStack：
   • 只存放当前栈中最小的元素。
   • 每当有新的元素入栈时，将当前最小元素也放入 minStack。
   • 每次出栈，都同步更新 minStack。

var MinStack = function () {
  this.stack = [] // 主栈存储所有元素
  this.minStack = [] // 辅助栈存储当前最小元素
}

/**
 * @param {number} val
 * @return {void}
 */
MinStack.prototype.push = function (val) {
  this.stack.push(val)
  // 如果 minStack 为空或当前值小于等于 minStack 顶部元素，将其加入 minStack
  if (this.minStack.length === 0 || val <= this.getMin()) {
    this.minStack.push(val)
  }
}

/**
 * @return {void}
 */
MinStack.prototype.pop = function () {
  const popped = this.stack.pop()
  // 如果出栈的元素等于当前最小元素，也从 minStack 中移除
  if (popped === this.getMin()) {
    this.minStack.pop()
  }
}

/**
 * @return {number}
 */
MinStack.prototype.top = function () {
  return this.stack[this.stack.length - 1]
}

/**
 * @return {number}
 */
MinStack.prototype.getMin = function () {
  return this.minStack[this.minStack.length - 1]
}

/**
 * Your MinStack object will be instantiated and called as such:
 * var obj = new MinStack()
 * obj.push(val)
 * obj.pop()
 * var param_3 = obj.top()
 * var param_4 = obj.getMin()
 */

5.2.LRU 缓存

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

思路：

• 使用一个**哈希表（map）**存储缓存数据。

• 使用一个

  双向链表

  来维护访问顺序：

  • 链表中越靠近头部的元素表示最近使用。
  • 链表中越靠近尾部的元素表示最久未使用。

• 当访问 get 或执行 put 操作时，需要移动元素到链表头部。

• 当达到容量限制并插入新元素时，移除链表尾部的元素（即最久未使用的元素）。

/**
 * @param {number} capacity
 */
var LRUCache = function (capacity) {
  this.capacity = capacity
  this.cache = new Map()
  this.head = {}
  this.tail = {}
  this.head.next = this.tail
  this.tail.prev = this.head
}

/**
 * @param {number} key
 * @return {number}
 */
LRUCache.prototype.get = function (key) {
  if (!this.cache.has(key)) return -1

  // 将访问的节点移动到链表头部
  const node = this.cache.get(key)
  this.removeNode(node)
  this.addToHead(node)

  return node.value
}

/**
 * @param {number} key
 * @param {number} value
 * @return {void}
 */
LRUCache.prototype.put = function (key, value) {
  if (this.cache.has(key)) {
    // 如果key已存在，更新值并移动到链表头部
    const node = this.cache.get(key)
    node.value = value
    this.removeNode(node)
    this.addToHead(node)
  } else {
    // 如果key不存在，创建新节点
    const newNode = { key, value }
    this.cache.set(key, newNode)
    this.addToHead(newNode)

    // 如果超出容量，删除最久未使用的项（链表尾部）
    if (this.cache.size > this.capacity) {
      const tailNode = this.tail.prev
      this.removeNode(tailNode)
      this.cache.delete(tailNode.key)
    }
  }
}

// 辅助方法：从链表中删除节点
LRUCache.prototype.removeNode = function (node) {
  node.prev.next = node.next
  node.next.prev = node.prev
}

// 辅助方法：将节点添加到链表头部
LRUCache.prototype.addToHead = function (node) {
  node.next = this.head.next
  node.prev = this.head
  this.head.next.prev = node
  this.head.next = node
}

5.3. O(1) 的数据结构

请你设计一个用于存储字符串计数的数据结构，并能够返回计数最小和最大的字符串。

实现 AllOne 类：

• AllOne() 初始化数据结构的对象。
• inc(String key) 字符串 key 的计数增加 1 。如果数据结构中尚不存在 key ，那么插入计数为 1 的 key 。
• dec(String key) 字符串 key 的计数减少 1 。如果 key 的计数在减少后为 0 ，那么需要将这个 key 从数据结构中删除。测试用例保证：在减少计数前，key 存在于数据结构中。
• getMaxKey() 返回任意一个计数最大的字符串。如果没有元素存在，返回一个空字符串 "" 。
• getMinKey() 返回任意一个计数最小的字符串。如果没有元素存在，返回一个空字符串 "" 。

**注意：**每个函数都应当满足 O(1) 平均时间复杂度。

示例：

输入
["AllOne", "inc", "inc", "getMaxKey", "getMinKey", "inc", "getMaxKey", "getMinKey"]
[[], ["hello"], ["hello"], [], [], ["leet"], [], []]
输出
[null, null, null, "hello", "hello", null, "hello", "leet"]

解释
AllOne allOne = new AllOne();
allOne.inc("hello");
allOne.inc("hello");
allOne.getMaxKey(); // 返回 "hello"
allOne.getMinKey(); // 返回 "hello"
allOne.inc("leet");
allOne.getMaxKey(); // 返回 "hello"
allOne.getMinKey(); // 返回 "leet"

数据结构设计：

我们将使用以下数据结构来保证所有操作在 O(1) 平均时间复杂度：

1. Hash Map：
   • keyToCount: 存储字符串到其计数之间的映射。
2. Doubly Linked List（桶结构）：
   • 使用桶来存储具有相同计数的字符串。
   • 每个桶表示一个计数值。
   • 每个桶中包含多个字符串。
   • 头尾两个虚节点： 帮助快速访问最大和最小计数的字符串。

var AllOne = function () {
  this.keyToCount = new Map() // 存储字符串到计数映射。
  this.countToKeys = new Map() // 存储每个计数值对应的字符串集合。
  this.head = { prev: null, next: null, count: Infinity, keys: new Set() }
  this.tail = { prev: null, next: null, count: -Infinity, keys: new Set() }
  this.head.next = this.tail
  this.tail.prev = this.head
}

AllOne.prototype.inc = function (key) {
  let count = (this.keyToCount.get(key) || 0) + 1
  this.keyToCount.set(key, count)

  let prevCount = count - 1
  if (this.countToKeys.has(prevCount)) {
    this.countToKeys.get(prevCount).delete(key)
    if (this.countToKeys.get(prevCount).size === 0) {
      this.countToKeys.delete(prevCount)
    }
  }

  if (!this.countToKeys.has(count)) {
    this.countToKeys.set(count, new Set())
  }
  this.countToKeys.get(count).add(key)
}

AllOne.prototype.dec = function (key) {
  let count = this.keyToCount.get(key)

  if (count === 1) {
    this.keyToCount.delete(key)
  } else {
    this.keyToCount.set(key, count - 1)
  }

  let prevCount = count - 1
  if (this.countToKeys.has(count)) {
    this.countToKeys.get(count).delete(key)
    if (this.countToKeys.get(count).size === 0) {
      this.countToKeys.delete(count)
    }
  }

  if (prevCount > 0) {
    if (!this.countToKeys.has(prevCount)) {
      this.countToKeys.set(prevCount, new Set())
    }
    this.countToKeys.get(prevCount).add(key)
  }
}

AllOne.prototype.getMaxKey = function () {
  if (this.countToKeys.size === 0) return ''
  const maxCount = Math.max(...this.countToKeys.keys())
  return Array.from(this.countToKeys.get(maxCount))[0]
}

AllOne.prototype.getMinKey = function () {
  if (this.countToKeys.size === 0) return ''
  const minCount = Math.min(...this.countToKeys.keys())
  return Array.from(this.countToKeys.get(minCount))[0]
}

const obj = new AllOne()
obj.inc('a')
obj.inc('b')
obj.inc('c')
console.log(obj.getMaxKey()) // 输出 "c"
console.log(obj.getMinKey()) // 输出 "a"

六.拓展练习

6.1.x 的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

**注意：**不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

思路

本题利用二分查找来求解，一开始把右边界粗略的设定为目标值 x，左右边界的中间值设为 mid，然后在二分过程中每次发现 mid * mid < x 的情况，就把这个 mid 值记录为 ans。

如果计算出的乘积正好等于 x，就直接返回这个 mid 值。

如果二分查找超出边界了，无论最后的边界是停留在小于 x 的位置还是大于 x 的位置，都返回 ans 即可，因为它是最后一个乘积小于 x 的值，一定是正确答案。

/**
 * @param {number} x
 * @return {number}
 */
var mySqrt = function (x) {
  let left = 0
  let right = x

  let ans = -1
  while (left <= right) {
    let mid = Math.round((left + right) / 2)
    let product = mid * mid
    if (product <= x) {
      ans = mid
      left = mid + 1
    } else if (product > x) {
      right = mid - 1
    } else {
      return mid
    }
  }

  return ans
}

6.2.UTF-8 编码验证

给定一个表示数据的整数数组 data ，返回它是否为有效的 UTF-8 编码。

UTF-8 中的一个字符可能的长度为 1 到 4 字节，遵循以下的规则：

1. 对于 1 字节 的字符，字节的第一位设为 0 ，后面 7 位为这个符号的 unicode 码。
2. 对于 n 字节 的字符 (n > 1)，第一个字节的前 n 位都设为1，第 n+1 位设为 0 ，后面字节的前两位一律设为 10 。剩下的没有提及的二进制位，全部为这个符号的 unicode 码。

这是 UTF-8 编码的工作方式：

      Number of Bytes  |        UTF-8 octet sequence
                       |              (binary)
   --------------------+---------------------------------------------
            1          | 0xxxxxxx
            2          | 110xxxxx 10xxxxxx
            3          | 1110xxxx 10xxxxxx 10xxxxxx
            4          | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx

x 表示二进制形式的一位，可以是 0 或 1。

**注意：**输入是整数数组。只有每个整数的 最低 8 个有效位 用来存储数据。这意味着每个整数只表示 1 字节的数据。

示例 1：

输入：data = [197,130,1]
输出：true
解释：数据表示字节序列:11000101 10000010 00000001。
这是有效的 utf-8 编码，为一个 2 字节字符，跟着一个 1 字节字符。

示例 2：

输入：data = [235,140,4]
输出：false
解释：数据表示 8 位的序列: 11101011 10001100 00000100.
前 3 位都是 1 ，第 4 位为 0 表示它是一个 3 字节字符。
下一个字节是开头为 10 的延续字节，这是正确的。
但第二个延续字节不以 10 开头，所以是不符合规则的。

思路：

1. 遍历数组中的字节。
2. 对每个字节：
   • 使用二进制表示并检查其最高位。
3. 根据最高位的值：
   • 如果最高位为 0：表示当前是单字节字符。
   • 如果最高位是 1
     • 统计需要多少个字节（即确定是 UTF-8 编码的字符长度）。
     • 验证接下来的字节是否符合连续字节的开头都为 10。
4. 如果符合 UTF-8 的所有规则，返回 true，否则返回 false。

/**
 * @param {number[]} data
 * @return {boolean}
 */
var validUtf8 = function (data) {
  let i = 0
  const n = data.length

  while (i < n) {
    let num = data[i]
    let bytesCount = 0

    // Determine the number of bytes in the current character
    if (num >> 7 === 0) {
      // 1-byte character (starting with 0)
      bytesCount = 1
    } else if (num >> 5 === 0b110) {
      // 2-byte character (starting with 110)
      bytesCount = 2
    } else if (num >> 4 === 0b1110) {
      // 3-byte character (starting with 1110)
      bytesCount = 3
    } else if (num >> 3 === 0b11110) {
      // 4-byte character (starting with 11110)
      bytesCount = 4
    } else {
      return false // Invalid first byte
    }

    // Check if we have enough remaining bytes
    if (i + bytesCount - 1 >= n) {
      return false
    }

    // Verify the continuation bytes
    for (let j = 1; j < bytesCount; j++) {
      if (data[i + j] >> 6 !== 0b10) {
        return false
      }
    }

    // Move to the next character
    i += bytesCount
  }

  return true
}

// Test examples
console.log(validUtf8([197, 130, 1])) // Output: true
console.log(validUtf8([235, 140, 4])) // Output: false

第二高的薪水

Employee 表：

+-------------+------+
| Column Name | Type |
+-------------+------+
| id          | int  |
| salary      | int  |
+-------------+------+
id 是这个表的主键。
表的每一行包含员工的工资信息。

查询并返回 Employee 表中第二高的 不同 薪水 。如果不存在第二高的薪水，查询应该返回 null(Pandas 则返回 None) 。

查询结果如下例所示。

示例 1：

输入：
Employee 表：
+----+--------+
| id | salary |
+----+--------+
| 1  | 100    |
| 2  | 200    |
| 3  | 300    |
+----+--------+
输出：
+---------------------+
| SecondHighestSalary |
+---------------------+
| 200                 |
+---------------------+

示例 2：

输入：
Employee 表：
+----+--------+
| id | salary |
+----+--------+
| 1  | 100    |
+----+--------+
输出：
+---------------------+
| SecondHighestSalary |
+---------------------+
| null                |
+---------------------+

方法：

1. 使用子查询或窗口函数来找到不同行中的薪水。
2. 使用 DISTINCT 关键字确保薪水是唯一的。
3. 按降序排列薪水。
4. 使用 LIMIT 和 OFFSET 选择第二高的薪水。

SELECT
    (SELECT DISTINCT salary
     FROM Employee
     ORDER BY salary DESC
     LIMIT 1 OFFSET 1) AS SecondHighestSalary;